Atcoder Beginner Contest 401 + 402 题解

发表于 2025-04-17 更新于 2025-04-24 分类于 Atcoder 阅读次数：本文字数： 9.6k

蓝桥杯前立的flag：打完蓝桥杯后就改掉 using namespace std 的习惯。又一年暑假前集训要开始啦，好好加油吧。

AtCoder Beginner Contest 401 题解

C

题意

定义一个数组：前 \(K\) 个元素都是 1，后面的元素为它前面 \(K\) 个元素的和，求第 \(N\) 项。

题解

不难想到通过前缀和维护，不过这里要注意 \(N,K\) 的大小没有指定，需要特判。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

const i64 mod = 1e9;

void solve() {
    int N, K;
    std::cin >> N >> K;
    if (N + 1 < K) {
        std::cout << 1 << "\n";
        return;
    }
    std::vector<i64> A(N + 2), pre(N + 2);
    for (int i = 1; i <= K; i++) {
        A[i] = 1;
        pre[i] = pre[i - 1] + A[i];
        pre[i] %= mod;
    }
    for (int i = K + 1; i <= N + 1; i++) {
        A[i] = pre[i - 1] - pre[i - 1 - K];
        A[i] %= mod;
        A[i] = (A[i] + mod) % mod;
        pre[i] = pre[i - 1] + A[i];
        pre[i] %= mod;
        pre[i] = (pre[i] + mod) % mod;
    }
    std::cout << A[N + 1] << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int t = 1;
    // std::cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

D

题意

一个含有 “?”、“.”、“o” 的字符串，可以将 "?" 变为 "o" 或 "."，要求 "o" 之间不能相邻，且转变后要恰好拥有 \(K\) 个 “o”，给出转变后的字符串，如果某位置的 “?” 取二者均可，保留它。

题解

一个直接的想法是，如果问号周围有 “o”，那么它的位置一定确定，剩下的看当前 “o” 的数目是否已经达到 \(K\)，如果达到了，剩下的问号都取 “.”，否则随意取。但是，这样的做法有一个问题：例如当 \(K = 3\) 时，字符串 “?????” 是确定的 “o.o.o”，但是我们的想法会输出原串，这是因为问号之间的限制，导致了一些情况必须要间隔取两种字符。我们遍历每一段全是问号的串，它们最大能贡献的 "o" 的数量是长度除以 2（向上取整）。我们应当用这样贡献的长度与 \(K\) 比较大小，如果相等，就必须这么极限地取，即对于长度为奇数的问号串，必须是 "o.o.o" 的形式。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    int N, K;
    std::cin >> N >> K;
    std::string S;
    std::cin >> S;
    S = " " + S;
    for (int i = 1; i <= N; i++) {
        if (S[i] == 'o') {
            S[i - 1] = '.';
            if (i + 1 <= N) {
                S[i + 1] = '.';
            }
        }
    }
    int cnt = std::count(S.begin() + 1, S.end(), 'o');
    if (cnt == K) {
        std::replace(S.begin(), S.end(), '?', '.');
        std::cout << S.substr(1) << "\n";
        return 0;
    }
    for (int l = 1; l <= N; l++) {
        if (S[l] == '?') {
            int r = l;
            while (r <= N && S[r] == '?') {
                r++;
            }
            cnt += (r - l + 1) / 2;
            l = r;
        }
    }
    if (cnt == K) {
        for (int l = 1; l <= N; l++) {
            if (S[l] == '?') {
                int r = l;
                while (r <= N && S[r] == '?') {
                    r++;
                }
                if ((r - l) % 2 == 1) {
                    for (int i = l; i < r; i++) {
                        S[i] = "o."[(i - l) % 2];
                    }
                }
                l = r;
            }
        }
    }
    std::cout << S.substr(1) << "\n";
    return 0;
}

E

题意

给定一个图，对于所有 \(1\le i\le N\)，求从 1 节点开始，恰好且只能到达 \(1,2,...i\) 所需要删掉的节点数，不存在则输出 -1。

题解

我们需要维护连通性，想到了并查集，对于一个已经满足答案的连通块，我们需要删除的点数就是这个连通块里面所有的连向的其他点。那么我们对于每一个 \(i\)，合并比自己小的节点，对于比自己大且未被访问过的节点，我们就会删除它，可以打上标记，在 \(i\) 等于它时清除。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

struct DSU {
    int n;
    std::vector<int> p, sz;
    DSU(int n_) {
        n = n_;
        init(n);
    }
    void init(int n) {
        p.resize(n + 1);
        sz.resize(n + 1, 1);
        std::iota(p.begin() + 1, p.end(), 1);
    }
    int find(int x) {
        while (x != p[x]) {
            x = p[x] = p[p[x]];
        }
        return x;
    }
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        if (sz[x] > sz[y]) {
            std::swap(x, y);
        }
        sz[y] += sz[x];
        p[x] = y;
        return true;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    int size(int x) { return sz[find(x)]; }
};

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    int N, M;
    std::cin >> N >> M;
    std::vector<std::vector<int>> e(N + 1);
    for (int i = 1; i <= M; i++) {
        int x, y;
        std::cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);
    }
    int ans = 0;
    DSU dsu(N);
    std::vector<bool> vis(N + 1);
    for (int i = 1; i <= N; i++) {
        if (vis[i]) {
            ans--;
        }
        for (auto y : e[i]) {
            if (y < i) {
                dsu.merge(y, i);
            } else if (!vis[y]) {
                vis[y] = true;
                ans++;
            }
        }
        if (dsu.size(i) == i) {
            std::cout << ans << "\n";
        } else {
            std::cout << -1 << "\n";
        }
    }

    return 0;
}

F

题意

给定两棵树，在两棵树的两点之间加一条边形成一条大树，记 \(f(i,j)\) 为连接第一棵树的 \(i\) 节点和第二棵树的 \(j\) 节点形成的树的直径（任意两点之间的最长简单路径），求 \(\sum_{i=1}^{N_1}\sum_{j=1}^{N_2}f(i,j)\)。

题解

合并两棵树后的直径，可能是之前两棵树的最大直径，也可能是 \(i\) 到这棵树的最远点的距离 + \(j\) 到第二棵树的最远点的距离 + 1。对于后一种情况，我们可以求出每个点到最远点的距离。一个结论是：树上的点能到达的最远点一定是某一条直径的端点。那么，我们可以找出一条直径，然后求出每个点能到达的最远距离 \(f_i\)。

求直径的办法是：两次 DFS / BFS 找最远点，那么两次找到的最远点就是一对直径的端点了。

然后，对于求和问题，我们采用排序 + 双指针的办法，找出 \(f1_i + f2_i + 1 > \max(dia1,dia2)\) 的位置，然后分头求和。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

auto solve() {
    int N;
    std::cin >> N;
    std::vector<std::vector<int>> adj(N + 1);
    for (int i = 1; i < N; i++) {
        int x, y;
        std::cin >> x >> y;
        adj[x].push_back(y);
        adj[y].push_back(x);
    }
    std::vector<int> f(N + 1);
    std::vector<int> dis(N + 1, -1);
    auto bfs = [&](int s) {
        std::queue<int> q;
        q.push(s);
        dis.assign(N + 1, -1);
        dis[s] = 0;
        while (!q.empty()) {
            int x = q.front();
            q.pop();
            for (auto y : adj[x]) {
                if (dis[y] == -1) {
                    dis[y] = dis[x] + 1;
                    q.push(y);
                }
            }
        }
        return std::max_element(dis.begin() + 1, dis.end()) - dis.begin();
    };
    auto a = bfs(1);
    auto b = bfs(a);
    f = dis;
    bfs(b);
    for (int i = 1; i <= N; i++) {
        f[i] = std::max(f[i], dis[i]);
    }
    return std::pair(f[b], f);
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    auto [dia1, f1] = solve();
    auto [dia2, f2] = solve();

    i64 ans = 0;
    int n1 = f1.size() - 1;
    int n2 = f2.size() - 1;
    std::sort(f1.begin() + 1, f1.end());
    std::sort(f2.begin() + 1, f2.end());
    int dia = std::max(dia1, dia2);
    i64 sum = 0;

    for (int i = 1, j = n2; i <= n1; i++) {
        while (j >= 1 && f1[i] + f2[j] + 1 > dia) {
            sum += f2[j];
            j--;
        }
        ans += 1ll * (n2 - j) * (f1[i] + 1) + sum;
        ans += 1ll * j * dia;
    }
    std::cout << ans << "\n";

    return 0;
}

Tokio Marine & Nichido Fire Insurance Programming Contest 2025 (AtCoder Beginner Contest 402) 题解

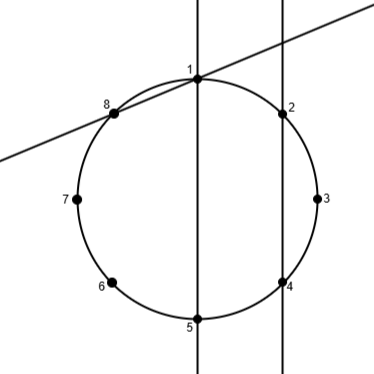
D

题意

给定一个正 \(n\) 边形和一些直线，每条直线连接两个顶点，求这些直线之间的交点个数。

题解

只要不平行就会相交，那么我们只要记录下每类平行直线的个数，枚举时每条直线加上之前直线的总条数减去此类与它平行的直线的条数即可。

至于平行的判断，容易发现是两端点之和相等，但是对于下图中 \((6,8)(2,4)\) 就不成立了。

我们发现 2 的逆时针走两个点本来应该是 0 的，因此，我们在两端点之和模 \(N\) 下进行处理即可。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    int N, M;
    std::cin >> N >> M;
    std::vector<std::array<int, 2>> A(M + 1);
    std::vector<int> X(N + 1);
    i64 ans = 0, all = 0;
    for (int i = 1; i <= M; i++) {
        int x, y;
        std::cin >> x >> y;
        A[i] = {x, y};
        ans += all - X[(x + y) % N];
        all++;
        X[(x + y) % N]++;
    }
    std::cout << ans << "\n";

    return 0;
}

E

题意

\(N\) 道题，每道题做对得 \(S_i\) 分，需要耗费 \(C_i\) 的精力，且做出来的概率是 \(P_i\)，给定初始精力，求最大得分。（每道题多次做对只给一题的分）

\(N\le 8\)

题解

\(N\) 如此小的数据范围，可以状压或者 \(O(N!)\) 暴力搜索。

状压的话我们考虑 \(dp_{i,\{S\}}\) 为精力为 \(i\) 时，只做集合 \(\{S\}\) 内的题所能获得的最大得分，那么转移我们枚举集合内的题是否做出来，转移方程为

\(dp_{i,\{S\}} = \max(dp_{i,\{S\}},(dp_{i-c_j,\{S/j\}} + S_j)\times P_j + (1-P_j)\times (dp_{i-c_j,\{S\}}))\)。

时间复杂度 \(O(NX2^N)\)

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    int N, X;
    std::cin >> N >> X;
    std::vector<int> S(N + 1), C(N + 1), P(N + 1);
    for (int i = 1; i <= N; i++) {
        std::cin >> S[i] >> C[i] >> P[i];
    }
    std::vector dp(X + 1, std::vector<double>(1 << N));
    for (int i = 0; i <= X; i++) {
        for (int j = 0; j < 1 << N; j++) {
            for (int k = 1; k <= N; k++) {
                if ((j >> (k - 1) & 1) && i >= C[k]) {
                    dp[i][j] = std::max(
                        dp[i][j], (dp[i - C[k]][j - (1 << (k - 1))] + S[k]) *
                                          P[k] / 100.0 +
                                      dp[i - C[k]][j] * (100 - P[k]) / 100.0);
                }
            }
        }
    }
    std::cout << std::fixed << std::setprecision(10) << dp[X][(1 << N) - 1]
              << "\n";

    return 0;
}

F

题意

一个 \(N\times N\) 的矩阵，从左上角走到右下角，只能向右或向下，把路径上依次经过的数连在一起看做一个长度 \(2N-1\) 的数，求这个数对 \(M\) 取模的最大值。

\(N\le 20\)

题解

暴力枚举是 \(O(2^{2N})\) 的，不够，不过这样的数据范围很容易让我们想到可以通过的 meet in the middle，它的复杂度是 \(O(N2^N)\)。

把整个数连起来再取模等价于把每个数拆开成十的幂乘基数，分开取模后相加，因此我们可以预处理每个位置乘十的幂后取模的结果，从左上角到主对角线搜一次，再从右下角到主对角线搜一次，将到达位置相同的值记录下来，通过排序 + 双指针的思想，要么是两边都取最大值，要么是在不超过 \(M\) 的情况下枚举答案。

时间复杂度\(O(N2^N + 2^N\log N)\)

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);

    int n, m;
    std::cin >> n >> m;
    std::vector<int> pow(2 * n);
    pow[0] = 1;
    for (int i = 1; i <= 2 * n - 1; i++) {
        pow[i] = pow[i - 1] * 10ll % m;
    }
    std::vector a(n + 1, std::vector<int>(n + 1));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            std::cin >> a[i][j];
            a[i][j] = 1ll * a[i][j] * pow[2 * n - i - j] % m;
        }
    }
    std::vector<std::vector<int>> L(n + 1), R(n + 1);
    auto dfs1 = [&](auto dfs1, int x, int y, int v) {
        v = (v + a[x][y]) % m;
        if (x + y == n + 1) {
            L[x].push_back(v);
            return;
        }
        dfs1(dfs1, x, y + 1, v);
        dfs1(dfs1, x + 1, y, v);
    };
    dfs1(dfs1, 1, 1, 0);
    auto dfs2 = [&](auto dfs2, int x, int y, int v) {
        if (x + y == n + 1) {
            R[x].push_back(v);
            return;
        }
        v = (v + a[x][y]) % m;
        dfs2(dfs2, x, y - 1, v);
        dfs2(dfs2, x - 1, y, v);
    };
    dfs2(dfs2, n, n, 0);
    int ans = 0;
    for (int x = 1; x <= n; x++) {
        std::sort(L[x].begin(), L[x].end());
        std::sort(R[x].begin(), R[x].end());
        ans = std::max(ans, L[x].back() + R[x].back() - m);
        for (int i = L[x].size() - 1, j = 0; i >= 0; i--) {
            while (j < R[x].size() && L[x][i] + R[x][j] < m) {
                ans = std::max(ans, L[x][i] + R[x][j]);
                j++;
            }
        }
    }
    std::cout << ans << "\n";
    return 0;
}