动态规划 暴力 dp 刷题

发表于 更新于 分类于 阅读次数： 本文字数： 25k
题目来自洛谷题单 https://www.luogu.com.cn/training/13993。

线性 dp

[P1095 NOIP 2007 普及组] 守望者的逃离

如果时间足够长，不够 10 魔力就休息，够 10 魔力就闪现一定是最优的，优先这么做。但是这样对于一些情况并不是最优的，需要再遍历一次，把第 \(i\) 次改为跑步来比较大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int m, s, t;
    cin >> m >> s >> t;
    int dis = 0, r = 17, f = 60;
    vector<int> dp(t + 1);
    for (int i = 1; i <= t; i++) {
        if (m >= 10) {
            dp[i] = dp[i - 1] + f;
            m -= 10;
        } else {
            m += 4;
            dp[i] = dp[i - 1];
        }
    }
    for (int i = 1; i <= t; i++) {
        dp[i] = max(dp[i], dp[i - 1] + 17);
        if (dp[i] >= s) {
            cout << "Yes\n" << i << "\n";
            return;
        }
    }
    cout << "No\n";
    cout << dp[t] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

P1077 摆花

方案数的 dp，思维可以一步一步由暴搜到记忆化搜索，再到 dp 转化而来。

暴搜显然就是枚举每一种花当前选几个，将状态（当前是在选第几种花和已经选了的数量）传递下去，然后从当前状态继续搜索下一种花，到搜索结束统计答案。

在记忆化下，我们可以存储搜过的状态，即 \(f_{i,j}\) 代表选第 \(i\) 种花，一共选了 \(j\) 朵花的答案，这也为我们 dp 提供了思路：设 \(dp_{i,j}\) 为前 \(i\) 种花，一共选择了 \(j\) 朵的方案数，那么状态转移显然有 \(dp_{i,j} = dp_{i,j} + dp_{i-1, j -k}\)，我们枚举当前第 \(i\) 种花选了 \(0\le k\le\min(a_i,j)\) 朵，就能在 \(O(nma)\) 的复杂度求出答案。另外，我们发现 \(dp_{i}\) 完全来自于 \(dp_{i-1}\) ，可以滚动数组优化空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

void solve() {
    int n, m;
    cin >> n >> m;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    vector<Z> mdp(m + 1);
    mdp[0] = 1;
    for (int i = 1; i <= n; i++) {
        vector<Z> dp(m + 1);
        for (int j = 0; j <= m; j++) {
            for (int k = 0; k <= min(a[i], j); k++) {
                dp[j] += mdp[j - k];
            }
        }
        mdp = dp;
    }
    cout << mdp[m] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P3842 TJOI2007]线段

数据范围不够 \(O(n^2)\)，还是只能考虑 \(O(n)\) 的做法。考虑到在一条线段中间往下走需要从两边走到中间，等价于从两端向下走再走到中间，所以我们只考虑走到两边的情况即可。设 \(dp_{i,0}\) 为走到第 \(i\) 行最左边的最短路径，\(dp_{i, 1}\) 为走到第 \(i\) 行最右边的最短路径，那么转移时也只用考虑从上一行的左右端点转移过来。

如果到达当前行左边，从上一行的左边转移过来，最好的方式就是先走到该行右边，再从右边走到左边；如果从上一行的右边转移过来也是相同的，先到右边再到左边。到达当前行右边同理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    cin >> n;
    vector<int> L(n + 1), R(n + 1);
    vector<array<int, 2>> dp(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> L[i] >> R[i];
    }
    dp[1][0] = R[1] - 1 + R[1] - L[1], dp[1][1] = R[1] - 1;
    for (int i = 2; i <= n; i++) {
        dp[i][0] = min(dp[i - 1][0] + abs(R[i] - L[i - 1]) + R[i] - L[i] + 1,
                       dp[i - 1][1] + abs(R[i] - R[i - 1]) + R[i] - L[i] + 1);
        dp[i][1] = min(dp[i - 1][0] + abs(L[i] - L[i - 1]) + R[i] - L[i] + 1,
                       dp[i - 1][1] + abs(L[i] - R[i - 1]) + R[i] - L[i] + 1);
    }
    cout << min(dp[n][0] + abs(n - L[n]), dp[n][1] + abs(n - R[n])) << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P1541 NOIP 2010 提高组] 乌龟棋

每种卡片的数量不超过 40，一共只有四种卡片，那么暴力设 \(dp_{i,j,k,l}\) 为分别取 \(i,j,k,l\) 张值为 1、2、3、4 的卡片暴力转移即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int dp[45][45][45][45];

void solve() {
    int n, m;
    cin >> n >> m;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    vector<int> s(5);
    for (int i = 1; i <= m; i++) {
        int x;
        cin >> x;
        s[x]++;
    }
    dp[0][0][0][0] = a[1];
    for (int i = 0; i <= s[1]; i++) {
        for (int j = 0; j <= s[2]; j++) {
            for (int k = 0; k <= s[3]; k++) {
                for (int l = 0; l <= s[4]; l++) {
                    int id = i + 2 * j + 3 * k + 4 * l + 1;
                    if (i) {
                        dp[i][j][k][l] =
                            max(dp[i][j][k][l], dp[i - 1][j][k][l] + a[id]);
                    }
                    if (j) {
                        dp[i][j][k][l] =
                            max(dp[i][j][k][l], dp[i][j - 1][k][l] + a[id]);
                    }
                    if (k) {
                        dp[i][j][k][l] =
                            max(dp[i][j][k][l], dp[i][j][k - 1][l] + a[id]);
                    }
                    if (l) {
                        dp[i][j][k][l] =
                            max(dp[i][j][k][l], dp[i][j][k][l - 1] + a[id]);
                    }
                }
            }
        }
    }
    cout << dp[s[1]][s[2]][s[3]][s[4]] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P4059 Code+#1] 找爸爸

由于空格的存在是比较难处理的，如果我们设 \(dp_{i,j}\) 直接进行 dp 的话，就需要分类讨论当前是否字符相同，字符不同就需要比较 A，B，以及本身的 \(d(x,y)\) 的大小，非常难处理，而且遇到相同的情况下后续也会出问题，我们的状态定义必须要把空格考虑进去。

在处理 \(dp_{i,j}\) 时，我们只需要考虑当前空格的影响：第一个字符串取空格、第二个取空格、都取、都不取，一共四种情况，但是都不取空格的话，显然比都取空格更优，因此只需要考虑前三种情况。设 \(dp_{i,j,0/1/2}\) 分别代表不取空格，第一个字符串取，第二个字符串取的最大值，那么 \(dp_{i,j,0} = \max(dp_{i-1,j-1,0/1/2} + d(x,y))\)

\(dp_{i,j,1} = \max(dp_{i,j-1,0/2} - A,dp_{i,j-1,1} - A)\)

\(dp_{i,j,2} = \max(dp_{i-1,j,0/1} - A,dp_{i-1,j,2} - B)\)。

注意初始化的时候 \(dp_{0,0,0} = 0, dp_{i,0,2} = -A - B(k-1), dp_{0,j,1} = - A - B(k-1)\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    string s, t;
    cin >> s >> t;
    int n = s.size(), m = t.size();
    s = " " + s;
    t = " " + t;
    vector<vector<int>> v(5, vector<int>(5));
    for (int i = 1; i <= 4; i++) {
        for (int j = 1; j <= 4; j++) {
            cin >> v[i][j];
        }
    }
    int A, B;
    cin >> A >> B;
    map<char, int> mp;
    mp['A'] = 1, mp['T'] = 2, mp['G'] = 3, mp['C'] = 4;
    for (int i = 1; i <= n; i++) {
        s[i] = mp[s[i]];
    }
    for (int i = 1; i <= m; i++) {
        t[i] = mp[t[i]];
    }
    vector<vector<vector<int>>> dp(
        n + 1, vector<vector<int>>(m + 1, vector<int>(3, -1e9)));
    dp[0][0][0] = 0;
    for (int i = 1; i <= m; i++) {
        dp[0][i][1] = -A - B * (i - 1);
    }
    for (int i = 1; i <= n; i++) {
        dp[i][0][2] = -A - B * (i - 1);
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            dp[i][j][0] =
                *max_element(dp[i - 1][j - 1].begin(), dp[i - 1][j - 1].end()) +
                v[s[i]][t[j]];
            dp[i][j][1] = max({dp[i][j - 1][1] - B, dp[i][j - 1][2] - A,
                               dp[i][j - 1][0] - A});
            dp[i][j][2] = max({dp[i - 1][j][1] - A, dp[i - 1][j][2] - B,
                               dp[i - 1][j][0] - A});
        }
    }
    cout << *max_element(dp[n][m].begin(), dp[n][m].end()) << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

背包 dp

P1833 樱花

完全背包 + 多重背包，完全背包正向枚举容量，直接从 dp 数组更新，多重背包使用单调队列优化，总时间复杂度为 \(O(nW)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    char c;
    int sth, stm, edh, edm, n;
    cin >> sth >> c >> stm >> edh >> c >> edm >> n;
    int W = (edh - sth) * 60 + (edm - stm);
    vector<int> w(n + 1), v(n + 1), k(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> v[i] >> k[i];
    }
    vector<int> dp(W + 1), mdp(W + 1);
    for (int i = 1; i <= n; i++) {
        if (k[i] == 0) {
            for (int j = w[i]; j <= W; j++) {
                dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
            }
        } else {
            for (int j = 0; j < w[i]; j++) {
                deque<int> q;
                int pos = 0;
                for (int x = 0; x * w[i] + j <= W; x++) {
                    while (pos <= x) {
                        while (!q.empty() &&
                               mdp[j + pos * w[i]] - pos * v[i] >
                                   mdp[j + q.back() * w[i]] - q.back() * v[i]) {
                            q.pop_back();
                        }
                        q.push_back(pos);
                        pos++;
                    }
                    while (!q.empty() && x - q.front() > k[i]) {
                        q.pop_front();
                    }
                    if (!q.empty()) {
                        dp[j + x * w[i]] = mdp[j + q.front() * w[i]] -
                                           q.front() * v[i] + x * v[i];
                    }
                }
            }
        }
        mdp = dp;
    }
    cout << dp[W] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P1064 NOIP 2006 提高组] 金明的预算方案

每一类商品（主件及其附件）一共有五种情况：都取，取主件和其中一个附件 1，取主件和其中一个附件 2，主件和两个附件都取，都不取，进行转移，设 \(dp_{i,j}\) 为 取前 \(i\) 个，容量为 \(j\) 的最大值转移即可，可以复制 dp 数组压掉一维。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int W, n;
    cin >> W >> n;
    vector<int> w(n + 1), v(n + 1), a(n + 1);
    vector<array<int, 3>> e(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> v[i] >> a[i];
        if (a[i] == 0) {
            e[i][0] = i;
        } else if (e[a[i]][1]) {
            e[a[i]][2] = i;
        } else {
            e[a[i]][1] = i;
        }
    }
    vector<int> dp(W + 1), mdp(W + 1);
    for (int i = 1; i <= n; i++) {
        for (int j = W; j >= 0; j--) {
            auto [f1, f2, f3] = e[i];
            dp[j] = max(dp[j], mdp[j]);
            if (f1 && j >= w[f1]) {
                dp[j] = max(dp[j], mdp[j - w[f1]] + w[f1] * v[f1]);
            }
            if (f2 && j >= (w[f1] + w[f2])) {
                dp[j] = max(dp[j], mdp[j - w[f1] - w[f2]] + w[f1] * v[f1] +
                                       w[f2] * v[f2]);
            }
            if (f3 && j >= (w[f1] + w[f3])) {
                dp[j] = max(dp[j], mdp[j - w[f1] - w[f3]] + w[f1] * v[f1] +
                                       w[f3] * v[f3]);
            }
            if (f2 && f3 && j >= (w[f1] + w[f2] + w[f3])) {
                dp[j] =
                    max(dp[j], mdp[j - w[f1] - w[f2] - w[f3]] + w[f1] * v[f1] +
                                   w[f2] * v[f2] + w[f3] * v[f3]);
            }
        }
        mdp = dp;
    }
    cout << dp[W] << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P1941 NOIP 2014 提高组] 飞扬的小鸟

容易想到设 \(dp_{i,j}\) 为到达第 \(i\) 列高度为 \(j\) 的位置需要的最少点击次数，那么考虑转移：如果不进行操作，就有 \(dp_{i,j} = dp_{i-1,j+y_{i-1}} + 1\)，如果进行操作，由于操作是可以进行任意次的，是一个完全背包问题，如果从高度为 \(k\) 的位置操作一次转移而来，应该有 \(dp_{i,j} = \min(dp_{i-1,k}, dp_{i,k}) + 1\)，同时注意高度超过 \(m\) 时会变为 \(m\)，也就是对于到达高度 \(m\) 的状态，可以由前面任意可行状态转移而来。

注意初始化把不可行的位置设为无穷大，以及 \(x,y\) 数组是从 0 开始的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n, m, k;
    cin >> n >> m >> k;
    vector<int> x(n + 1), y(n + 1);
    for (int i = 0; i < n; i++) {
        cin >> x[i] >> y[i];
    }
    vector<array<int, 3>> a(k + 1);
    for (int i = 1; i <= k; i++) {
        cin >> a[i][0] >> a[i][1] >> a[i][2];
    }
    sort(a.begin() + 1, a.end());
    vector<vector<int>> dp(n + 1, vector<int>(m + 1, 1e9));
    for (int j = 1; j <= m; j++) {
        dp[0][j] = 0;
    }
    int p = 1;
    for (int i = 1; i <= n; i++) {
        int lo = 1, hi = m;
        if (p <= k && a[p][0] == i) {
            lo = a[p][1] + 1, hi = a[p][2] - 1;
            p++;
        }
        for (int j = 1; j <= hi; j++) {
            for (int k = j - x[i - 1]; k <= m; k++) {
                if (k > j - x[i - 1] && j < m) {
                    break;
                }
                if (k >= 1) {
                    dp[i][j] = min(dp[i][j], min(dp[i - 1][k], dp[i][k]) + 1);
                }
            }
        }
        for (int j = lo; j <= hi; j++) {
            if (j + y[i - 1] <= m) {
                dp[i][j] = min(dp[i][j], dp[i - 1][j + y[i - 1]]);
            }
        }
        for (int j = 1; j <= lo - 1; j++) {
            dp[i][j] = 1e9;
        }
    }
    int ans = 1e9;
    for (int i = 1; i <= m; i++) {
        ans = min(ans, dp[n][i]);
    }
    if (ans != 1e9) {
        cout << 1 << "\n";
        cout << ans << "\n";
        return;
    }
    ans = 0;
    for (int i = 1; i <= k; i++) {
        bool ok = false;
        for (int j = a[i][1] + 1; j <= a[i][2] - 1; j++) {
            if (dp[a[i][0]][j] != 1e9) {
                ans++;
                ok = true;
                break;
            }
        }
        if (!ok) {
            cout << 0 << "\n";
            cout << ans << "\n";
            return;
        }
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P2340 USACO03FALL] Cow Exhibition G

求两者之和的最大值的一个套路是：我们转化为枚举其中一个值的范围，求出另一个值的最大值，求出二者之和的最大值。这里我们把智商固定下来，求情商就是一个 01 背包问题代表取或不取。但是考虑到会有负数的背包容量，转移时会超出值域范围，我们考虑把背包容量扩大两倍，把中间值设为初始态。同时注意在压缩一维的情况下正数需要倒序转移，负数需要正序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    cin >> n;
    vector<int> s(n + 1), t(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> s[i] >> t[i];
    }
    vector<int> dp(800001, -1e9);
    dp[400000] = 0;
    for (int i = 1; i <= n; i++) {
        if (s[i] >= 0) {
            for (int j = 800000; j >= s[i]; j--) {
                dp[j] = max(dp[j], dp[j - s[i]] + t[i]);
            }
        } else {
            for (int j = 0; j <= 800000 + s[i]; j++) {
                dp[j] = max(dp[j], dp[j - s[i]] + t[i]);
            }
        }
    }
    int ans = 0;
    for (int i = 400000; i <= 800000; i++) {
        if (dp[i] > 0) {
            ans = max(ans, dp[i] + i - 400000);
        }
    }
    cout << ans << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

区间 dp

[P1880 NOI1995] 石子合并

最经典的区间 dp，这里稍微提一下区间 dp 的套路：

区间 dp 的状态一般是设 \(dp_{i,j}\) 为区间 \([i,j]\) 的答案，那么转移方程就是枚举 \(k\in[i,j)\)，\(dp_{i,j} = \max(dp_{i,k} + dp_{k+1,r})\) + 区间合并的代价。本题合并的代价就是 \(\sum_{i=l}^{r}a_i\)，可以使用前缀和优化。

对于环形，考虑破环成链，求出 \([1,2n]\) 区间的答案然后取长为 \(n\) 的区间取最值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    cin >> n;
    vector<int> a(2 * n + 1), pre(2 * n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i + n] = a[i];
    }
    for (int i = 1; i <= 2 * n; i++) {
        pre[i] = pre[i - 1] + a[i];
    }
    vector<vector<int>> dp(2 * n + 1, vector<int>(2 * n + 1, 1e9));
    for (int i = 1; i <= 2 * n; i++) {
        dp[i][i] = 0
    }
    for (int len = 2; len <= 2 * n; len++) {
        for (int l = 1; l + len - 1 <= 2 * n; l++) {
            int r = l + len - 1;
            for (int k = l; k < r; k++) {
                dp[l][r] = min(dp[l][r],
                               dp[l][k] + dp[k + 1][r] + pre[r] - pre[l - 1]);
            }
        }
    }
    int ans = 1e9;
    for (int i = 1; i <= n; i++) {
        ans = min(ans, dp[i][i + n - 1]);
    }
    cout << ans << "\n";
    dp.assign(2 * n + 1, vector<int>(2 * n + 1, 0));
    for (int len = 2; len <= 2 * n; len++) {
        for (int l = 1; l + len - 1 <= 2 * n; l++) {
            int r = l + len - 1;
            for (int k = l; k < r; k++) {
                dp[l][r] = max(dp[l][r],
                               dp[l][k] + dp[k + 1][r] + pre[r] - pre[l - 1]);
            }
        }
    }
    ans = 0;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, dp[i][i + n - 1]);
    }
    cout << ans << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P3146 USACO16OPEN] 248 G

合并相邻两个数想到区间 dp，这里设 \(dp_{l,r}\) 为经过合并后区间边缘的最大值（注意不是区间内的最值，而是两个区间合并后才能取最大值，否则不能合并的最大值会作为答案转移），如果 \([l,r]\) 之间没有任何区间能合并，这个区间的答案就是 0 。因此，最终答案不是 \(dp_{1,n}\)，需要我们在合并过程中取最值。转移方程为 \(dp_{l,r} = \max(dp_{l,k} + 1)\)，要求 \(dp_{l,k} = dp_{k+1,r} > 0\)（等于 0 会被错误合并）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    vector<vector<int>> dp(n + 1, vector<int>(n + 1));
    for (int i = 1; i <= n; i++) {
        dp[i][i] = a[i];
    }
    int ans = *max_element(a.begin() + 1, a.end());
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            for (int k = l; k < r; k++) {
                if (dp[l][k] == dp[k + 1][r] && dp[l][k] > 0) {
                    dp[l][r] = max(dp[l][r], dp[l][k] + 1);
                }
                ans = max(ans, dp[l][r]);
            }
        }
    }
    cout << ans << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P1063 NOIP 2006 提高组] 能量项链

设 \(dp_{l,r}\) 为区间 \([l,r]\) 能获得的最大值，那么我们枚举中间分割点 \(k\)，自然需要把 \([l,k],[k+1,r]\) 合并，转移方程为 \(dp_{l,r} = \max(dp_{l,k} + dp_{k+1, r} + a[l][0] * a[k][1] * a[r][1])\)（用 \(a_{i,0/1}\) 分别表示取该位置的头 / 尾）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    cin >> n;
    vector<array<int, 2>> a(2 * n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i][0];
        a[i + n][0] = a[i][0];
    }
    for (int i = 2; i <= 2 * n; i++) {
        a[i - 1][1] = a[i][0];
    }
    a[2 * n][1] = a[1][0];
    vector<vector<i64>> dp(2 * n + 1, vector<i64>(2 * n + 1));
    for (int len = 2; len <= 2 * n; len++) {
        for (int l = 1; l + len - 1 <= 2 * n; l++) {
            int r = l + len - 1;
            for (int k = l; k < r; k++) {
                dp[l][r] = max(dp[l][r], dp[l][k] + dp[k + 1][r] +
                                             a[l][0] * a[k][1] * a[r][1]);
            }
        }
    }
    i64 ans = 0;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, dp[i][i + n - 1]);
    }
    cout << ans << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

[P4342 IOI 1998] Polygon

看似是很常规的区间取最大值，但是可能会有两个负数相乘得到最大值的情况，因此除了维护最大值，还要维护最小值，更新时四种情况取最值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    cin >> n;
    vector<int> a(2 * n + 1), op(2 * n + 1);
    for (int i = 1; i <= n; i++) {
        char x;
        cin >> x;
        op[i] = (x == 't' ? 0 : 1);
        cin >> a[i];
        op[i + n] = op[i];
        a[i + n] = a[i];
    }
    vector<vector<int>> f(2 * n + 1, vector<int>(2 * n + 1, -1e9));
    vector<vector<int>> g(2 * n + 1, vector<int>(2 * n + 1, 1e9));
    for (int i = 1; i <= 2 * n; i++) {
        f[i][i] = g[i][i] = a[i];
    }
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= 2 * n; l++) {
            int r = l + len - 1;
            for (int k = l; k < r; k++) {
                if (op[k + 1] == 0) {
                    f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r]);
                    g[l][r] = min(g[l][r], g[l][k] + g[k + 1][r]);
                } else {
                    f[l][r] = max({f[l][r], f[l][k] * f[k + 1][r],
                                   f[l][k] * g[k + 1][r], g[l][k] * f[k + 1][r],
                                   g[l][k] * g[k + 1][r]});
                    g[l][r] = min({g[l][r], f[l][k] * f[k + 1][r],
                                   f[l][k] * g[k + 1][r], g[l][k] * f[k + 1][r],
                                   g[l][k] * g[k + 1][r]});
                }
            }
        }
    }
    int ans = -1e9;
    for (int i = 1; i <= n; i++) {
        ans = max(ans, f[i][i + n - 1]);
    }
    cout << ans << "\n";
    vector<int> v;
    for (int i = 1; i <= n; i++) {
        if (f[i][i + n - 1] == ans) {
            v.push_back(i);
        }
    }
    for (auto x : v) {
        cout << x << " ";
    }
    cout << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

CF149D

状态转移非常特殊，首先区间不是合法括号串是没有意义的，我们选择从两端进行记忆化搜索，保证搜到的答案是有意义的。同时，由于合并两个区间需要知道相邻的颜色，我们需要额外的状态，设 \(dp_{i,j,0/1/2,0/1/2}\)，后两维分别代表左右端的颜色。

基准情况：两括号相邻，此时即 “（）” 的情况，只能一个空白一个涂色。而如果两括号是匹配的（“ (()) ”），也是一个空白一个涂色，中间取不相邻的颜色更新即可。如果不相邻（“(())(())”），就找左右括号的匹配位置，拆成两部分答案相乘。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
#include <bits/stdc++.h>
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变
string s;
int n;
vector<int> pos;
Z dp[701][701][3][3];

void dfs(int l, int r) {
    if (l + 1 == r) {
        dp[l][r][0][1] = dp[l][r][0][2] = dp[l][r][1][0] = dp[l][r][2][0] = 1;
        return;
    }
    if (pos[l] == r) {
        dfs(l + 1, r - 1);
        for (int i = 0; i <= 2; i++) {
            for (int j = 0; j <= 2; j++) {
                if (j != 1) {
                    dp[l][r][0][1] += dp[l + 1][r - 1][i][j];
                }
                if (j != 2) {
                    dp[l][r][0][2] += dp[l + 1][r - 1][i][j];
                }
                if (i != 1) {
                    dp[l][r][1][0] += dp[l + 1][r - 1][i][j];
                }
                if (i != 2) {
                    dp[l][r][2][0] += dp[l + 1][r - 1][i][j];
                }
            }
        }
    } else {
        dfs(l, pos[l]);
        dfs(pos[l] + 1, r);
        for (int i = 0; i <= 2; i++) {
            for (int j = 0; j <= 2; j++) {
                for (int p = 0; p <= 2; p++) {
                    for (int q = 0; q <= 2; q++) {
                        if ((j == p && p == 1) || (j == p && p == 2)) {
                            continue;
                        }
                        dp[l][r][i][q] +=
                            dp[l][pos[l]][i][j] * dp[pos[l] + 1][r][p][q];
                    }
                }
            }
        }
    }
}

void solve() {
    cin >> s;
    n = s.size();
    s = " " + s;
    pos.resize(n + 1);
    vector<int> stk;
    for (int i = 1; i <= n; i++) {
        if (s[i] == '(') {
            stk.push_back(i);
        } else {
            pos[stk.back()] = i;
            stk.pop_back();
        }
    }
    dfs(1, n);
    Z ans = 0;
    for (int i = 0; i <= 2; i++) {
        for (int j = 0; j <= 2; j++) {
            ans += dp[1][n][i][j];
        }
    }
    cout << ans << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

UVA12991 Game Rooms

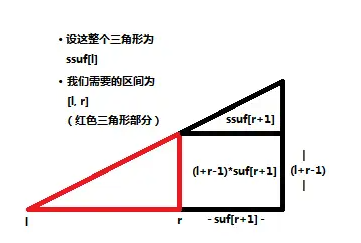
本题不是直接的区间 dp，但是利用了区间的思想。我们知道，最终答案一定是将 \([1, n]\) 分成了若干区间，这些区间分别放置乒乓桌和泳池，那么对于每一段，我们只需要统计这一段的人到另一个设施的最短距离。设 \(dp_{i,0/1}\) 为前 \(i\) 层，第 \(i\) 层放置了乒乓球桌 / 泳池的最短距离和，那么转移我们可以枚举 \(j\)，那么 \([j+1,i]\) 就全部放置我们选择的设施，状态转移方程为 \(dp_{i,0/1} = dp_{j,1/0} + cost(j+1, i)\)。接下来考虑 cost 的计算：显然我们把这些层分为两半，下面的去下面的区域最优，上面的就去上面的区域，那么我们只需要求出二阶前后缀和即可（参考下面的图片，把 $l + r -1 $ 改为 \(r - l + 1\)）。

image-20250409174500756

状压 dp

省选（洛谷紫题）难度的先跳过吧...

插头 dp

怎么敢碰瓷的...

数位 dp