ACM七月训练 & UESTC 暑假一轮集训

发表于 更新于 分类于 阅读次数： 本文字数： 93k
又到了暑假一轮，希望今年能弥补去年的遗憾吧。

7 月 9 日 Round-1

集训的第一场队内赛，还没开始时还蛮紧张的，不知道相比去年进步了多少。一开始不知道题目按顺序来的，先去看了一些后面的题发现难以战胜，然后看了眼榜发现有人过 A 了就开始写，依稀记得一个结论，手玩了个样例后就大胆交了，通过。然后继续看 B，琢磨样例后发现就是因数分解，可惜没考虑完全，没有特判，在 debug 半天后吃了两发罚时。C 题倒是过的很快，然后看了眼 D ，一眼没啥想法就去看 E 了，殊不知这是本场最错的一个决定。

在 E 题写了个线段树过样例后交上去 WA 了，然后浪费太多时间发现做法假了，这时才去看 C，理清楚后在 2 小时 30 多分过了，但是罚时也上去了，最终 rnk 12 / 36。

E

题意

给定两个排列 \(p\) 和 \(q\)，将 \(p_1,p_2,...,p_n\) 依次放入盒子，现在进行 \(n\) 轮，第 \(i\) 轮（\(1\le i < n\)）让 \(q_1,q_2,...,q_{i-1}\)​ 的位置安装炸弹，每次放入一个带有炸弹的数后，就会炸掉盒子里最大的数，求每一轮全部放入后剩余的最大值。

\(n \le 3\times 10^5\)

题解

容易发现答案是非递增的，考虑什么时候会发生变化。

一开始，我们的答案就是 \(n\)，因为第一轮没有数被炸掉。如果我们当前的答案 \(x\) 能够保留的话，说明至少存在一个位置 \(i\) 满足在这个位置及它的后面，“ \(\ge x\)” 的数要严格多于这些位置“炸弹的数量”，这样的话，炸弹就会优先炸掉更大的数，而不是 \(x\)。而一旦不存在这样的位置后，我们的答案就要减少，一直减少到存在这样的位置。

考虑怎么维护这样的位置，我们可以通过线段树来维护，节点存放“当前位置及它的后面，“\(\ge x\) 的数量”减去“炸弹的数量”，这样，我们通过查询整个区间的最大值即可。具体地，在 \(q_i\) 位置放一个炸弹，说明 \([1, q_i]\) 的右边会多一个炸弹，区间整体减 1，我们的答案 \(x\) 减少，就要更新区间 \([1,pos[x]]\)，因为它们右边 \(\ge x\)​ 的数量增加了。

时间复杂度：\(O(n\log n)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class Info, class Tag>
struct LazySegmentTree {
    int n;
    std::vector<Info> info;
    std::vector<Tag> tag;
    LazySegmentTree() : n(0) {}
    LazySegmentTree(int n_, Info v_ = Info()) { init(n_, v_); }
    template <class T>
    LazySegmentTree(std::vector<T> init_) {
        init(init_);
    }
    void init(int n_, Info v_ = Info()) { init(std::vector(n_ + 1, v_)); }
    template <class T>
    void init(std::vector<T> init_) {
        n = init_.size() - 1;
        info.assign(4 * (n + 1), Info());
        tag.assign(4 * (n + 1), Tag());
        std::function<void(int, int, int)> build = [&](int p, int l, int r) {
            if (l == r) {
                info[p] = Info(init_[l]);
                return;
            }
            int mid = (l + r) / 2;
            build(2 * p, l, mid);
            build(2 * p + 1, mid + 1, r);
            pull(p);
        };
        build(1, 1, n);
    }
    void pull(int p) { info[p] = info[2 * p] + info[2 * p + 1]; }
    void apply(int p, const Tag &v) {
        info[p].apply(v);
        tag[p].apply(v);
    }
    void push(int p) {
        apply(2 * p, tag[p]);
        apply(2 * p + 1, tag[p]);
        tag[p] = Tag();
    }
    void modify(int p, int l, int r, int x, const Info &v) {
        if (l == r) {
            info[p] = v;
            return;
        }
        int mid = (l + r) / 2;
        push(p);
        if (x <= mid) {
            modify(2 * p, l, mid, x, v);
        } else {
            modify(2 * p + 1, mid + 1, r, x, v);
        }
        pull(p);
    }
    void modify(int x, const Info &v) { modify(1, 1, n, x, v); }
    Info rangeQuery(int p, int l, int r, int x, int y) {
        if (l > y || r < x) {
            return Info();
        }
        if (x <= l && r <= y) {
            return info[p];
        }
        push(p);
        int mid = (l + r) / 2;
        return rangeQuery(2 * p, l, mid, x, y) +
               rangeQuery(2 * p + 1, mid + 1, r, x, y);
    }
    Info rangeQuery(int l, int r) { return rangeQuery(1, 1, n, l, r); }
    void rangeApply(int p, int l, int r, int x, int y, const Tag &v) {
        if (l > y || r < x) {
            return;
        }
        if (x <= l && r <= y) {
            apply(p, v);
            return;
        }
        int mid = (l + r) / 2;
        push(p);
        rangeApply(2 * p, l, mid, x, y, v);
        rangeApply(2 * p + 1, mid + 1, r, x, y, v);
        pull(p);
    }
    void rangeApply(int l, int r, const Tag &v) {
        rangeApply(1, 1, n, l, r, v);
    }
    template <class F>
    int findFirst(int p, int l, int r, int x, int y, F &&pred) {
        if (l >= y || r <= x) {
            return -1;
        }
        if (l >= x && r <= y && !pred(info[p])) {
            return -1;
        }
        if (r - l == 1) {
            return l;
        }
        int m = (l + r) / 2;
        push(p);
        int res = findFirst(2 * p, l, m, x, y, pred);
        if (res == -1) {
            res = findFirst(2 * p + 1, m, r, x, y, pred);
        }
        return res;
    }
    template <class F>
    int findFirst(int l, int r, F &&pred) {
        return findFirst(1, 0, n, l, r, pred);
    }
    template <class F>
    int findLast(int p, int l, int r, int x, int y, F &&pred) {
        if (l >= y || r <= x) {
            return -1;
        }
        if (l >= x && r <= y && !pred(info[p])) {
            return -1;
        }
        if (r - l == 1) {
            return l;
        }
        int m = (l + r) / 2;
        push(p);
        int res = findLast(2 * p + 1, m, r, x, y, pred);
        if (res == -1) {
            res = findLast(2 * p, l, m, x, y, pred);
        }
        return res;
    }
    template <class F>
    int findLast(int l, int r, F &&pred) {
        return findLast(1, 0, n, l, r, pred);
    }
};

struct Tag {
    int x = 0;
    Tag() {}
    Tag(int x) : x(x) {}
    void apply(const Tag &v) { x += v.x; }
};

struct Info {
    int mx = 0;
    Info() {}
    Info(int v) : mx(v) {}
    void apply(const Tag &v) { mx += v.x; }
};

Info operator+(const Info &a, const Info &b) {
    Info info;
    info.mx = std::max(a.mx, b.mx);
    return info;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    std::cin >> n;
    std::vector<int> p(n + 1), q(n + 1), pos(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> p[i];
        pos[p[i]] = i;
    }
    for (int i = 1; i <= n; i++) {
        std::cin >> q[i];
    }
    LazySegmentTree<Info, Tag> seg(n);
    int ans = n;
    std::cout << ans;
    seg.rangeApply(1, pos[ans], Tag(1));
    for (int i = 1; i < n; i++) {
        seg.rangeApply(1, q[i], Tag(-1));
        while (seg.info[1].mx <= 0) {
            ans--;
            seg.rangeApply(1, pos[ans], Tag(1));
        }
        std::cout << " " << ans;
    }
    std::cout << "\n";

    return 0;
}

F

题意

\(n\) 个平台，每个平台都有颜色，一共 \(m\) 种，开始时所有平台都不能使用，可以使用 \(x_i\) 的代价，激活第 \(i\) 种颜色的所有平台。在行走时，可以从当前平台走到下一个或者下两个激活的平台，求从 1 走到 \(n\) 的最小代价。

\(n\le 3\times 10^5, m\le 40\)

题解

\(m = 40\) 的数据范围一定是突破口，这样的数字很容易联想到 meet in the middle。

我们对这 \(m\) 个颜色建图，如果在两个平台相邻，将它们对应的颜色连边。由于必须从当前平台走到下一个或者下两个激活的平台，因此图上所有边的两个端点都至少应该被激活一个，否则无法继续往下走——这样我们想到了最大权独立集问题。另外，如果相邻平台颜色相同，说明必须选择，起点和终点也连一条自环，代表必须选择。

这样处理，我们要求最小代价，就是代价总和减去最大权独立集了。有一个非常经典的做法：枚举前 \(m / 2\) 个点是否选择，对其余的 \(m / 2\) 个点记忆化搜索。

具体地，我们状压状态数，代表当前状态点最大权独立集，我们暴力搜索时，直接取最高位的颜色，枚举它选 / 不选作为最大权独立集的情况，如果选择，还应该满足它不存在自环，并且递归时排除掉与它相邻的点。这样一来，高位枚举是 \(O(2^{\frac{m}{2}})\) 的，而在低位，每个状态都只会被访问一次，也是 \(O(2^{\frac{m}{2}})\) 的，因此总体就是 \(O(2^{\frac{m}{2}})\)​​ 的。

时间复杂度：\(O(n + 2^{\frac{m}{2}})\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    std::vector<int> c(n + 1), x(m);
    for (int i = 1; i <= n; i++) {
        std::cin >> c[i];
        c[i]--;
    }
    for (int i = 0; i < m; i++) {
        std::cin >> x[i];
    }

    std::vector<i64> adj(m);
    std::vector<int> ban(m);
    for (int i = 1; i < n; i++) {
        if (c[i] == c[i + 1]) {
            ban[c[i]] = 1;
        }
        adj[c[i]] |= 1ll << c[i + 1];
        adj[c[i + 1]] |= 1ll << c[i];
    }
    ban[c[1]] = ban[c[n]] = 1;

    int ans = accumulate(x.begin(), x.end(), 0);
    std::vector<bool> vis(1 << 20);
    std::vector<int> f(1 << 20);
    auto dfs = [&](auto dfs, i64 S) {
        if (!S) {
            return 0;
        }
        if (S < (1 << 20) && vis[S]) {
            return f[S];
        }
        if (S < (1 << 20)) {
            vis[S] = true;
        }
        int p = 63 - __builtin_clzll(S);
        int res = dfs(dfs, S ^ (1ll << p));
        if (!ban[p]) {
            res = std::max(res, dfs(dfs, S ^ (1ll << p) ^ (S & adj[p])) + x[p]);
        }
        if (S < (1 << 20)) {
            f[S] = res;
        }
        return res;
    };

    std::cout << ans - dfs(dfs, (1ll << m) - 1) << "\n";

    return 0;
}

G

题意

给一个置换 \(p\) 染色，并定义置换的乘积 \(c = a\times b = b[a[i]]\)，幂为 \(p^k = p\times p\times ... \times p\)，定义无限路径为：\(i,p[i],p[p[i]],...\)，求最小的 \(k\)，满足 \(p^k\) 至少存在一条无限路径颜色都相同。

\(n\le 10^5\)

题解

首先想通过两道题区分一下运算：

ABC367E 运算为 \(B_i = A_{X_i}\)，将 \(i\) 向 \(p_i\) 连边，会得到若干个环，每次运算，相当于每个节点都向连的边移动。

ABC377E 运算为 \(P_i = P_{P_i}\)，这实际是一个复合运算 \(P\circ P\)，如果 \(P^\prime = P\circ P\)，那么再进行一次变换，实际是 \(P^\prime\circ P^\prime = (P\circ P) \circ (P\circ P) = P^4\)。

本题应该是前者。由于只要求一条无限路径，我们可以分开看各个环。

一个结论是，在长度为 \(n\) 的环上，从某个点出发，每次跳 \(k\) 个单位，最终能走到的点恰好等于每次跳 \(\gcd(n, k)\) 个单位能走到的点。

我们考虑环上的点是 \(\mathbb{Z}_n\)，即模 \(n\) 的整数集合。考虑乘法同余群 \(\mathbb{Z}_n\) 中由 \(k\) 生成的子群： \[ \langle k \rangle = \{ jk \bmod n : j \in \mathbb{Z} \} \] 这是一个加法子群，其元素个数为：

​
\[ \left| \langle k \rangle \right| = \frac{n}{\gcd(n, k)} \] 这意味着：从 \(0\) 出发，每次加 \(k\)，mod \(n\) 形成的循环节长度为 \(\frac{n}{\gcd(n, k)}\)

即：

​ 在 \(\mathbb{Z}_n\) 中，\(k\) 生成的同余类是 \(\langle k \rangle\)，它的大小就是 \(\frac{n}{\gcd(n, k)}\)

因为 \(\gcd(n, k) \mid k\)，所以： \[ \langle k \rangle = \langle d \rangle, \quad \text{其中 } d = \gcd(n, k) \] 那么，我们枚举环长的因数，然后 \(O(n)\) 判断是否符合条件即可。

时间复杂度：\(O(n\sqrt{n})\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    std::cin >> n;
    std::vector<int> p(n + 1), c(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> p[i];
    }
    for (int i = 1; i <= n; i++) {
        std::cin >> c[i];
    }
    int ans = n;
    std::vector<bool> vis(n + 1);
    for (int i = 1; i <= n; i++) {
        if (vis[i]) {
            continue;
        }
        std::vector<int> tmp;
        int j = i;
        while (!vis[j]) {
            vis[j] = true;
            tmp.push_back(j);
            j = p[j];
        }
        auto get = [&](std::vector<int> &a) {
            std::vector<int> d;
            int l = a.size();
            for (int i = 1; i * i <= l; i++) {
                if (l % i == 0) {
                    d.push_back(i);
                    if (i != l / i) {
                        d.push_back(l / i);
                    }
                }
            }
            sort(d.begin(), d.end());
            for (auto k : d) {
                for (int i = 0; i < k; i++) {
                    bool flag = true;
                    for (int j = i; j < l; j += k) {
                        flag &= c[a[j]] == c[a[i]];
                    }
                    if (flag) {
                        return k;
                    }
                }
            }
            return l;
        };
        ans = std::min(ans, get(tmp));
    }
    std::cout << ans << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int T;
    std::cin >> T;
    while (T--) {
        solve();
    }

    return 0;
}

一些 __builtin_函数的使用

  • __builtin_clz(x)：返回 \(x\) 的前导 0 的个数，31 - __builtin_clz(x) 可以求最高位 1 的位置，代替 __lg，注意对 0 使用未定义

  • __builtin_clzll(x)：前者的 long long 版本，以下函数都有，不再说明。

  • __builtin_popcount(x)：返回 \(x\) 二进制表示中 1 的个数，可以判断一个数是不是 2 的幂。

7 月 10 日 Round 2

lyc 场，糖丸了。

开局 8 分钟把 A 秒了当时排第二，然后坐牢三小时，B 题 WA 11，C 题 WA 5，都没有结果。最终 rank 28 / 36。但是今天补题收获蛮大的，还去学了一下三分。

rating 表也出来了，还需要加油呀。

B

题意

交互题，40 次询问。\([1, 10^5]\) 里有 \(n\) 个人，你可以询问一个位置，得出该位置到所有人的曼哈顿距离之和。找到任意一个人的具体位置。

题解

\(\sum\mid x - x_i\mid\) 是具有单峰性的（注意图像，不是突变的，唉怎么这里都想错了），确定最低点即可。

似乎三分就行，但是实际一想，\(2\lceil\log_{\frac{3}{2}}10^5\rceil\) 的询问次数会超过 40，因此不能三分。

但是它的导数具有单调性呀，也不用导，二分斜率就行了。每次询问一个位置与下一个位置的斜率，找到 \(< 0\) 与 \(> 0\) 的交界点即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    std::cin >> n;

    std::map<int, int> mp;
    int cnt = 0;
    auto query = [&](int x) {
        if (mp.count(x)) {
            return mp[x];
        }
        cnt++;
        std::cout << "? " << x << std::endl;
        int res = 0;
        std::cin >> res;
        mp[x] = res;
        return res;
    };
    auto answer = [&](int x) { std::cout << "! " << x << std::endl; };

    int lo = 1, hi = 1e5 - 1;
    int ans = 0;
    while (lo <= hi) {
        int mid = (lo + hi) / 2;
        int x = query(mid), y = query(mid + 1);
        if (y - x <= 0) {
            ans = mid;
            lo = mid + 1;
        } else {
            hi = mid - 1;
        }
    }

    answer(ans + 1);
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

C

题意

一棵树，选定 \(k\) 个点作为出发位置，向 1 号节点发出使者，其余的 \(n - k\) 个位置是旅游点，每个使者的满意度定义为到根节点的简单路径经过的旅游点之和，求最大满意度。

题解

教训：多数学推导公式，画树直觉分析时多画点子节点，不要只画二叉的。

如果我们要在一个节点发出使者，那么这个节点的儿子一定都发出了，不然答案不优。如果一个位置发出使者，贡献为到根节点的距离减去子树的大小再加上 1，我们求出贡献后排序，就知道要让哪些节点发出使者了，DFS 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k;
    std::cin >> n >> k;
    std::vector<std::vector<int>> adj(n + 1);
    for (int i = 1; i < n; i++) {
        int x, y;
        std::cin >> x >> y;
        adj[x].push_back(y);
        adj[y].push_back(x);
    }
    std::vector<int> dep(n + 1), sz(n + 1);
    auto dfs = [&](auto dfs, int x, int fa) -> void {
        sz[x] = 1;
        dep[x] = dep[fa] + 1;
        for (auto y : adj[x]) {
            if (y == fa) {
                continue;
            }
            dfs(dfs, y, x);
            sz[x] += sz[y];
        }
    };
    dfs(dfs, 1, 0);

    std::vector<std::array<int, 2>> d(n + 1);
    for (int i = 1; i <= n; i++) {
        d[i] = {dep[i] - sz[i], i};
    }
    sort(d.begin() + 1, d.end(), std::greater());
    std::vector<bool> indust(n + 1);
    for (int i = 1; i <= k; i++) {
        auto [_, id] = d[i];
        indust[id] = true;
    }

    i64 ans = 0;
    auto dfs2 = [&](auto dfs2, int x, int fa, int depth) -> void {
        for (auto y : adj[x]) {
            if (y == fa) {
                continue;
            }
            if (indust[y]) {
                ans += depth;
                dfs2(dfs2, y, x, depth);
            } else {
                dfs2(dfs2, y, x, depth + 1);
            }
        }
    };
    dfs2(dfs2, 1, 0, 1);
    std::cout << ans << "\n";

    return 0;
}

D

题意

给定 \(p, q, n\) ，要求构造长度为 \(n\) 的数组，满足任意连续 \(p\) 个数之和 $ > 0$，任意连续 \(q\) 个数 \(< 0\) 或输出不存在。

题解

收获：区间和可以多往前缀和考虑。

直接推导并没有很强的性质。但是如果用 \(S_i\) 代表前缀和的话，一定有 \(S_i < S_{i + p}, S_{i + q} < S_i\)，这是题目要求决定的。

那么，我们可以建立一张从 0 开始编号，有 \(n + 1\) 个节点的图，按照小于号连边，即 \(S_i\rightarrow S_{i + p}, S_{i+q}\rightarrow S_i\)，这样一来，我们可以通过拓扑序来为这些前缀和赋值，如果出现了环就说明不可能。

构造出前缀和后，我们通过差分即可求出最终答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int p, q, n;
    std::cin >> p >> q >> n;
    std::vector<std::vector<int>> adj(n + 1);
    std::vector<int> deg(n + 1);
    for (int i = 0; i + p <= n; i++) {
        adj[i].push_back(i + p);
        deg[i + p]++;
    }
    for (int i = 0; i + q <= n; i++) {
        adj[i + q].push_back(i);
        deg[i]++;
    }

    std::queue<std::array<int, 2>> que;
    for (int i = 0; i <= n; i++) {
        if (deg[i] == 0) {
            que.push({i, 0});
        }
    }

    if (que.empty()) {
        std::cout << "NO\n";
        return;
    }
    std::vector<int> pre(n + 1);
    int cnt = 0;
    while (!que.empty()) {
        auto [x, v] = que.front();
        pre[x] = v;
        que.pop();
        cnt++;
        for (auto y : adj[x]) {
            pre[y] = std::max(pre[y], v + 1);
            deg[y]--;
            if (deg[y] == 0) {
                que.push({y, v + 1});
            }
        }
    }
    if (cnt != n + 1) {
        std::cout << "NO\n";
        return;
    }
    std::cout << "YES\n";
    for (int i = 1; i <= n; i++) {
        std::cout << pre[i] - pre[i - 1] << " \n"[i == n];
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

E

题意

交互题。有长度为 \(n\) 的排列 $ p$ 和 \(2n\) 次询问次数。有两种操作：一种是选择一个 \(1\le x\le 2n\)，将满足 \(i + j = x\) 的点 \(i,j\) 连一条无向边，一种是选择两个下标 \(i,j\)，输出从 \(p_i\) 到 \(p_j\) 的最短路。求出这个排列（可以输出两个排列，只要其中一个正确即可）。

题解

边连边边求最短路是不现实的，询问次数完全不够，而我们最倾向的连边方式肯定是连成一条链，这样最短路也是排列，有利于我们确定答案，而想连成一条链，我们选择 \(x = n + 1\) 和 \(x = n + 2\) 即可，此时所有节点连成了一个螺旋状。询问次数 2 次。

然后我们可以任意选择一个节点，询问其余节点到它的最短路，这样我们就可以知道链条的其中一端（但是要非常注意，这里我们知道的仅仅是 \(p_i\) 对应的下标 \(i\) 而不是 \(p_i\)）。询问次数 \(n - 1\) 次。

接着，我们已知链条一端开始问，就能求出 \(ans_i\)，代表下标为 \(i\) 的排列 \(p_i\) 到我们指定的链条一端的距离是 \(ans_i - 1\)。询问次数 \(n - 1\)次。

现在，我们只知道每个下标，而不是排列，我们还要想办法求出具体的排列。我们的选择 \(x = n + 1\) 和 \(x = n + 2\) 其实具有很强的性质：它按螺旋状，从 1 开始，把到达链条一端距离为 $0,1,2，...，n - 1 $ 的排列依次放好。也就是说，\(ans_i = 1\) 对应的 \(p_i\) 一定会被放在 1 号位，\(ans_i = 2\) 对应的 \(p_i\) 一定会被放在 \(n\) 号位... 这样，我们即可恢复。

但是还需要注意的是，我们之前指定了链条一端，然而题目可能是以另一端开头的，因此把我们的 \(ans\) 数组反向后还有一种情况。

总的询问次数恰好是 \(2n\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    std::cin >> n;
    auto query = [&](int a, int b) {
        std::cout << "? " << a << " " << b << std::endl;
        int x;
        std::cin >> x;
        return x;
    };
    auto link = [&](int x) {
        std::cout << "+ " << x << std::endl;
        int p;
        std::cin >> p;
    };
    auto answer = [&](auto &v, auto &v2) {
        std::cout << "!";
        for (int i = 1; i <= n; i++) {
            std::cout << " " << v[i];
        }
        for (int i = 1; i <= n; i++) {
            std::cout << " " << v2[i];
        }
        std::cout << std::endl;
        int x;
        std::cin >> x;
    };
    link(n + 2);
    link(n + 1);
    std::vector<int> ans(n + 1);
    int p = 1, mx = 0;
    for (int i = 2; i <= n; i++) {
        int q = query(1, i);
        if (q > mx) {
            p = i;
            mx = q;
        }
    }
    ans[p] = 1;
    for (int i = 1; i <= n; i++) {
        if (i == p) {
            continue;
        }
        int q = query(p, i);
        ans[i] = q + 1;
    }

    std::vector<int> tmp(n + 1), tmp2(n + 1);
    int l = 1, r = n;
    std::vector<int> ord(n + 1);
    for (int i = 1; i <= n; i++) {
        if (i & 1) {
            ord[i] = l++;
        } else {
            ord[i] = r--;
        }
    }

    for (int i = 1; i <= n; i++) {
        tmp[i] = ord[ans[i]];
    }
    for (int i = 1; i <= n; i++) {
        tmp2[i] = ord[n - ans[i] + 1];
    }
    answer(tmp, tmp2);
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

F

题意

给定一张无向图，每条边有边权，以及一个整数阈值 \(V\)。\(q\) 次询问，每次给定 \(x,y\)，你需要判定是否存在一条 \(x\) 到 \(y\) 的边权 \(AND\) 和大于等于 \(V\)。

题解

这种涉及到位运算的一定是按位考虑，我们贪心地从高到低，考虑什么时候 \(x,y\) 能够满足条件，既然需要二者之间的路径 \(AND\) 大于等于 \(v\)，考虑每一条边，必然会在二进制下存在一个相同的位置 \(pos\)，满足 \(pos\) 的高位上与 \(v\) 完全一样，而在 \(pos\) 位上，\(v\) 的二进制都是 0 而边权的二进制都是 1，这样一定符合条件。还需要注意 \(v\) 恰好等于边权时的情况，此时也是成立的。

我们通过对每一位建立一个并查集，将满足上述条件的边合并，查询就是查询连通性。

时间复杂度：\(O((n + q)\log n\alpha(n))\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

struct DSU {
    int n;
    std::vector<int> p, sz;
    DSU(int n_) {
        n = n_;
        init(n);
    }
    void init(int n) {
        p.resize(n + 1);
        sz.resize(n + 1, 1);
        iota(p.begin() + 1, p.end(), 1);
    }
    int find(int x) {
        while (x != p[x]) {
            x = p[x] = p[p[x]];
        }
        return x;
    }
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        if (sz[x] > sz[y]) {
            std::swap(x, y);
        }
        sz[y] += sz[x];
        p[x] = y;
        return true;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    int size(int x) { return sz[find(x)]; }
};

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m, q;
    i64 v;
    std::cin >> n >> m >> q >> v;
    std::vector<std::array<i64, 3>> e(m + 1);
    std::vector<int> b(60);
    for (int i = 59; i >= 0; i--) {
        if (v >> i & 1) {
            b[i] = 1;
        }
    }
    std::vector<DSU> dsu(61, DSU(n));
    for (int i = 1; i <= m; i++) {
        i64 x, y, w;
        std::cin >> x >> y >> w;
        e[i] = {x, y, w};
        for (int j = 59; j >= 0; j--) {
            if (!(v >> j & 1) && (w >> j & 1)) {
                dsu[j].merge(x, y);
            } else if ((v >> j & 1) && !(w >> j & 1)) {
                break;
            }
            if ((w & v) == v) {
                dsu[60].merge(x, y);
            }
        }
    }
    while (q--) {
        int x, y;
        std::cin >> x >> y;
        bool ok = false;
        for (int i = 60; i >= 0; i--) {
            if (dsu[i].same(x, y)) {
                ok = true;
                break;
            }
        }
        if (ok) {
            std::cout << "Yes\n";
        } else {
            std::cout << "No\n";
        }
    }

    return 0;
}

7 月 11 日 Round 3

rzy 场，比昨天好，rank 21 / 36，可惜的是 B 题没有调出来，补题把没怎么学的组合数学好好学了一下。

B

题意

给定 \(n,k,a,b\) ，其中 \(a + b = n\)，构造一个字符串，要求有 \(a\) 个 G 和 \(b\) 个 B，且不能连续出现超过 \(k\) 个相同字母，或判断无解。

题解

从无解入手，容易想到的是如果按照连续的字符为一组的话，\(a\) 和 \(b\) 分别的组数范围是 \([\lceil \frac{a}{k}\rceil, a], [\lceil \frac{b}{k}\rceil, b]\)，我们构造的字符串，必须选择的组数相差不能超过 1，那么就可以判断无解了。

如果有解的话，不妨枚举 \(i\) 作为 \(a\) 的组数，求出满足条件的 \(b\) 对应的组数 \(j\)，然后求出每一组的长度，即 \(\lfloor\frac{a}{k}\rfloor\)，如果不能整除，则会有 \(a\pmod k\) 个组的长度为 \(\lfloor\frac{a}{k}\rfloor + 1\)，\(b\)​ 同理，然后输出即可。

我没有注意到 \(j > i\) 时应该以 \(i\) 为准输出 5555

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k, a, b;
    std::cin >> n >> k >> a >> b;

    if (a == 0) {
        if (k >= n) {
            for (int i = 1; i <= n; i++) {
                std::cout << 'B';
            }
            std::cout << "\n";
        } else {
            std::cout << "NO\n";
        }
        return 0;
    }

    if (b == 0) {
        if (k >= n) {
            for (int i = 1; i <= n; i++) {
                std::cout << 'G';
            }
            std::cout << "\n";
        } else {
            std::cout << "NO\n";
        }
        return 0;
    }

    if (b - (a + k - 1) / k >= -1 && a - (b + k - 1) / k >= -1) {
        for (int i = (a + k - 1) / k; i <= a; i++) {
            if ((b + k - 1) / k - 1 <= i && i <= b + 1) {
                int j;
                if ((b + k - 1) / k <= i && i <= b) {
                    j = i;
                } else if ((b + k - 1) / k - 1 == i) {
                    j = (b + k - 1) / k;
                } else {
                    j = b;
                }
                auto output = [&](char c, int len) {
                    for (int i = 1; i <= len; i++) {
                        std::cout << c;
                    }
                };
                assert(std::abs(i - j) <= 1);
                if (i >= j) {
                    int y = a % i, x = i - y;
                    int len1 = a / i + (y != 0 ? 1 : 0);
                    int q = b % j, p = j - q;
                    int len2 = b / j + (q != 0 ? 1 : 0);
                    int tot1 = 0, tot2 = 0;
                    if (y != 0) {
                        std::swap(x, y);
                    }
                    if (q != 0) {
                        std::swap(p, q);
                    }
                    for (int _ = 1; _ <= j; _++) {
                        if (tot1 < x) {
                            output('G', len1);
                        } else {
                            output('G', len1 - 1);
                        }
                        if (tot2 < p) {
                            output('B', len2);
                        } else {
                            output('B', len2 - 1);
                        }
                        tot1++, tot2++;
                    }
                    if (i > j) {
                        if (tot1 < x) {
                            output('G', len1);
                        } else {
                            output('G', len1 - 1);
                        }
                    }
                } else {
                    int y = a % i, x = i - y;
                    int len1 = a / i + (y != 0 ? 1 : 0);
                    int q = b % j, p = j - q;
                    int len2 = b / j + (q != 0 ? 1 : 0);
                    int tot1 = 0, tot2 = 0;
                    if (y != 0) {
                        std::swap(x, y);
                    }
                    if (q != 0) {
                        std::swap(p, q);
                    }
                    for (int _ = 1; _ <= i; _++) {
                        if (tot2 < p) {
                            output('B', len2);
                        } else {
                            output('B', len2 - 1);
                        }
                        if (tot1 < x) {
                            output('G', len1);
                        } else {
                            output('G', len1 - 1);
                        }
                        tot1++, tot2++;
                    }
                    if (tot2 < p) {
                        output('B', len2);
                    } else {
                        output('B', len2 - 1);
                    }
                }
                return 0;
            }
        }
    } else {
        std::cout << "NO\n";
    }
    return 0;
}

这么做对于 B 题还是太麻烦了，实际上我们判断无解后，每次贪心放最多的即可，同时计数不能超过 \(k\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k, a, b;
    std::cin >> n >> k >> a >> b;
    if (((a + k - 1) / k - 1 > b) || ((b + k - 1) / k - 1 > a)) {
        std::cout << "NO\n";
        return 0;
    }
    int tot = 0;
    int cnt[2] = {a, b};
    char c = 'G';
    for (int i = 1; i <= n; i++) {
        auto get = [&](char c) {
            if (c == 'B') {
                return 1;
            } else {
                return 0;
            }
        };
        if (tot < k && cnt[get(c)] >= cnt[!get(c)]) {
            tot++;
            std::cout << c;
            cnt[get(c)]--;
        } else {
            tot = 1;
            if (c == 'G') {
                c = 'B';
            } else {
                c = 'G';
            }
            std::cout << c;
            cnt[get(c)]--;
        }
    }

    return 0;
}

E

题意

给定 \(n,m,a,Q\)，初始时有一个长度为 \(n\) 的数组 \(A\)，每个元素都是 \(a\)，然后在模 \(Q\) 的条件下进行 \(m\) 轮迭代：依次对 \(1,2,...,n - 1\) 进行计算 \(A_i = A_i \times A_{i + 1}\)，求最终的数组。

\(1\le m,n \le \phi(a, Q)\le 10^6+123\)，其中 \(\phi(a, Q)\) 代表 \(a\) 在模 \(Q\) 条件下的阶，且保证这个数是素数。

题解

很奇怪的数据范围，手玩一下后我们很容易发现第 \(i\) 轮迭代，第 \(j\) 个位置的指数，记为 \(b_{i,j}\)，应该有 \(b_{i, j} = b_{i -1,j} + b_{i - 1, j + 1}\)，这跟组合数学中杨辉三角非常类似，又不完全一样的是，初始指数都是 1，因此求和会有差别。不过我们进行差分 \(c_j = b_j - b_{j+1}\) 后会惊讶的发现这就是杨辉三角，于是我们可以知道 \(b_{i,j} = \sum_{k = 0}^{n - j}\begin{pmatrix}i\\k\end{pmatrix}\)。

既然阶是一个素数，我们又只考虑了指数，所以求 \(b\) 完全可以在模 \(\phi(a,Q)\) 的条件下运算，最终答案依次求快速幂即可。

时间复杂度：\(O(n\log n)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int qpow(int a, int b, int mod) {
    int res = 1;
    while (b) {
        if (b & 1) {
            res = 1ll * res * a % mod;
        }
        a = 1ll * a * a % mod;
        b /= 2;
    }
    return res;
}

int inv(int a, int mod) { return qpow(a, mod - 2, mod); }

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m, a, Q;
    std::cin >> n >> m >> a >> Q;
    int mod = 1;
    for (int i = a % Q; i != 1; mod++) {
        i = 1ll * i * a % Q;
    }
    std::vector<int> frac(mod);
    frac[0] = 1;
    for (int i = 1; i < mod; i++) {
        frac[i] = 1ll * frac[i - 1] * i % mod;
    }
    std::vector<int> pre(std::max(n, m) + 1);
    pre[0] = 1;

    for (int i = 1; i <= m; i++) {
        pre[i] = (pre[i - 1] + 1ll * frac[m] * inv(frac[i], mod) % mod *
                                   inv(frac[m - i], mod) % mod) %
                 mod;
    }

    for (int i = m + 1; i <= n; i++) {
        pre[i] = pre[i - 1];
    }

    for (int i = n; i >= 1; i--) {
        std::cout << qpow(a, pre[i - 1], Q) << " \n"[i == 1];
    }

    return 0;
}

F

题意

给定一个矩阵，可以任意选择一些位置 + 1，要求相邻位置的数不能相同。

题解

诈骗题，这种相邻的具有很强的奇偶性，且奇偶性一致的各自彼此之间无影响，因此指定一个奇偶性即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int>> a(n + 1, std::vector<int>(m + 1));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            std::cin >> a[i][j];
        }
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if ((i + j) & 1) {
                if (a[i][j] % 2 == 0) {
                    a[i][j]++;
                }
            } else {
                if (a[i][j] % 2 == 1) {
                    a[i][j]++;
                }
            }
        }
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            std::cout << a[i][j] << " \n"[j == m];
        }
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

G

题意

在一个 \(n\times n\) 的棋盘放 \(n\) 个棋子，要求每个格子所在的一行或者一列至少有一个棋子，且互相能看见（中间不能有其他棋子）的棋子对有 \(k\) 对。对 998244353 取模。

题解

只能放 \(n\) 个棋子，且每个格子所在的一行或者一列至少有一个棋子，所以我们要么在每一行都放，要么在每一列都放，这两种情况是等价的，只考虑一种情况对答案数乘 2 即可。

不妨在每一行都放，这样的话能相互看见的棋子不会超过 \(n - 1\) 对，因此 \(k\ge n\) 时答案就是 0。\(k = 0\) 时也需要特判，因为此时行列会有相同的情况，答案就是 \(n!\)。

然后是一般情况，如果 \(k = 1\)，我们选择两个位置绑成一起，答案是 \(\begin{pmatrix}n\\2\end{pmatrix} (n -1)!\)，如果 \(k = 2\)，可以拆成 \(2 + 0\)，也可以是 \(1 + 1\)，分别对应 \(\begin{pmatrix}n\\3\end{pmatrix} (n -2)!\) 和 \(\begin{pmatrix}n\\2\end{pmatrix} \begin{pmatrix}n-2\\2\end{pmatrix}(n -2)!\)....这让我们想到了，我们需要将 \(n\) 个不同行的棋子，放进 \(n - k\) 个不同的列中，这是第二类斯特林数。记为\(\left\{ \begin{matrix} n\\n - k \end{matrix} \right\}\)，通项公式为 \(\left\{ \begin{matrix} n\\m\end{matrix} \right\} = \sum_{i = 0} ^ m\frac{(-1)^{m-i}i^n}{i!(m - i) !}\)。

因此，最终答案就是 \(2\left\{ \begin{matrix} n\\n - k\end{matrix} \right\}(n - k)!\)。

我们预处理阶乘及逆元，即可 \(O(n)\) 求出答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 998244353;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k;
    std::cin >> n >> k;
    if (k >= n) {
        std::cout << 0 << "\n";
        return 0;
    }

    std::vector<Z> frac(n + 1), invfrac(n + 1);
    frac[0] = frac[1] = invfrac[0] = invfrac[1] = Z(1);
    for (int i = 2; i <= n; i++) {
        frac[i] = frac[i - 1] * i;
    }
    invfrac[n] = power(frac[n], P - 2);
    for (int i = n - 1; i >= 1; i--) {
        invfrac[i] = invfrac[i + 1] * (i + 1);
    }

    if (k == 0) {
        std::cout << frac[n] << "\n";
        return 0;
    }

    auto S = [&](int n, int k) {
        Z ans = 0;
        for (int i = 0; i <= k; i++) {
            ans += power(Z(-1), k - i) * power(Z(i), n) * invfrac[i] *
                   invfrac[k - i];
        }
        return ans;
    };
    Z ans = S(n, n - k) * Z(2);
    for (int i = n; i > k; i--) {
        ans *= i;
    }
    std::cout << ans << "\n";

    return 0;
}

7 月 12 日 Round 4

rank 10 / 36，可惜的是细节写挂比较多（遍历矩阵 \(m\) 写成 \(n\)），吃了不少罚时，甚至写了对拍才发现，不过把我认为赛时能过的都做出来了，还是不错，晚上 ABC，有数论分块的题，正好重新学一下。

E

题意

\(n\) 个点，每次操作从所有点中随机抽 2 个，如果连边后这两个节点的度数都不超过 2，则连边。求直到不能操作时，操作次数的期望。

\(n\le 200\)

题解

期望 dp，设当前状态为 \(f_{W}\)，由 \(f_{W_i^\prime}\) 转移过来，每种转移又对应一个被选中的概率 \(p_i\)，除此之外，还有一些选法是不符合条件的，需要再选一次。那么应该有： \[ f_{W} = \sum(f_{W_i^\prime} + 1)p_i + (1 - \sum p_i)(f_W + 1) \]

合并后，有 \[ f_W = \frac{\sum(f_{W_i^\prime} + 1)p_i + 1 - \sum p_i}{\sum p_i} \] 而每次操作，我们选的点总情况数是 \(\frac{n^2}{2}\)（不考虑顺序），设每个概率 \(p_i\) 对应的选法为 \(A_i\)，有 \[ f_W = \frac{\sum(f_{W_i^\prime} + 1)A_i + \frac{n^2}{2} - \sum A_i}{\sum A_i} \] 然后考虑具体状态的设计，从数据范围来看应该是 \(O(n^3)\) 的，设计出来蛮需要脑子的可惜我没有。

在题目的限制下，我们连边后，这个图只会有孤立点、链和环。设 \(f_{i,j,k}\) 表示当前有 \(i\) 个孤立点，\(j\) 条长度为 2 的链，\(k\) 条长度 \(>2\) 的链，要区分链的长度，主要是因为要构成环的话，长度为 2 是不合法的。那么转移可能有：

  • 选择两个孤立的点，组成一条链，情况数为 \(\begin{pmatrix}i\\2\end{pmatrix}\)。
  • 选择一个孤立的点，和一条长度为 2 的链的两端之一，组成一条长度大于 2 的链，情况数为 \(2ij\)
  • 选择一个孤立的点，和一条长度大于 2 点链点两端之一，扩大这条链的长度，情况数为 \(2ik\)
  • 选择两条长度为 2 的链的两端之一，拼成一条长度大于 2 的链，情况数为 $2 \[\begin{pmatrix}j\\2\end{pmatrix}\] $
  • 选择一条长度为 2 的链的两端之一，再选择一条长度大于 2 的链的两端之一，拼成一条长度大于 2 的链，情况数 \(4jk\)
  • 选择两条长度大于 2 的链的两端之一，拼成一条长度大于 2 的链，情况数 $2 \[\begin{pmatrix}k\\2\end{pmatrix}\] $​
  • 选择一条长度大于 2 的链的两端，拼成一个环，情况数 \(k\)

然后套上面公式记忆化搜索 dp。

时间复杂度：\(O(n^3)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

constexpr int N = 210;
double f[N][N][N];
bool vis[N][N][N];
int n;
double dfs(int x, int y, int z) {
    if (vis[x][y][z] == true) {
        return f[x][y][z];
    }
    f[x][y][z] = 0;
    int sum = 0;
    if (x >= 2) {
        f[x][y][z] += (dfs(x - 2, y + 1, z) + 1) * x * (x - 1) / 2;
        sum += x * (x - 1) / 2;
    }
    if (x >= 1 && y >= 1) {
        f[x][y][z] += (dfs(x - 1, y - 1, z + 1) + 1) * 2 * x * y;
        sum += 2 * x * y;
    }
    if (x >= 1) {
        f[x][y][z] += (dfs(x - 1, y, z) + 1) * 2 * x * z;
        sum += 2 * x * z;
    }
    if (y >= 2) {
        f[x][y][z] += (dfs(x, y - 2, z + 1) + 1) * y * (y - 1) * 2;
        sum += y * (y - 1) * 2;
    }
    if (y >= 1) {
        f[x][y][z] += (dfs(x, y - 1, z) + 1) * 4 * y * z;
        sum += 4 * y * z;
    }
    if (z >= 1) {
        f[x][y][z] += (dfs(x, y, z - 1) + 1) * 2 * z * (z - 1);
        sum += 2 * z * (z - 1);
    }
    if (z >= 1) {
        f[x][y][z] += (dfs(x, y, z - 1) + 1) * z;
        sum += z;
    }
    f[x][y][z] += 1.0 * n * n / 2 - sum;
    f[x][y][z] /= sum;
    vis[x][y][z] = true;
    return f[x][y][z];
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    std::cin >> n;
    vis[0][0][0] = vis[1][0][0] = vis[0][1][0] = true;
    std::cout << std::fixed << std::setprecision(10) << dfs(n, 0, 0) << "\n";

    return 0;
}

F

题意

给定一个括号串，从 1 走到 \(n\)，可以走重复的字符，\(q\) 次查询，每次改变一个位置的字符，求是否能走出一个匹配的括号串。

题解

长度为奇数显然不行，只考虑偶数的情况。

手玩后可以发现，只要存在 “((” 的结构，不管后面我们需要多少个 “)”，总能走出需要的个数，反过来同理。因此我们只需要保证最左边的 “))” 的左边有 “((”，最右边的 “((” 右边有 “))”。我们可以记录每个这样的字符串的起始位置，通过一个 std::set 动态更新即可。如果没有上述的字符串出现，就要求这个串本身就是匹配的，而由于没有上述的字符串，说明 “(” 和 “)” 是交替出现的，只要求首尾正确即可。

时间复杂度：\(O((n + q)\log n)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, q;
    std::cin >> n >> q;
    std::string s;
    std::cin >> s;
    s = " " + s;

    std::set<int> L, R;
    for (int i = 1; i < n; i++) {
        if (s[i] == s[i + 1]) {
            if (s[i] == '(') {
                L.insert(i);
            } else {
                R.insert(i);
            }
        }
    }

    while (q--) {
        int p;
        std::cin >> p;
        if (n & 1) {
            std::cout << "NO\n";
            continue;
        }
        if (p + 1 <= n && s[p] == s[p + 1]) {
            if (s[p] == '(') {
                L.erase(p);
            } else {
                R.erase(p);
            }
        }
        if (p - 1 >= 1 && s[p] == s[p - 1]) {
            if (s[p - 1] == '(') {
                L.erase(p - 1);
            } else {
                R.erase(p - 1);
            }
        }

        if (s[p] == '(') {
            s[p] = ')';
        } else {
            s[p] = '(';
        }

        if (p + 1 <= n && s[p] == s[p + 1]) {
            if (s[p] == '(') {
                L.insert(p);
            } else {
                R.insert(p);
            }
        }
        if (p - 1 >= 1 && s[p] == s[p - 1]) {
            if (s[p - 1] == '(') {
                L.insert(p - 1);
            } else {
                R.insert(p - 1);
            }
        }
        if (s[1] == ')' || s[n] == '(') {
            std::cout << "NO\n";
        } else if (L.empty() && R.empty()) {
            std::cout << "YES\n";
        } else if (L.empty() || R.empty()) {
            std::cout << "NO\n";
        } else if (*L.begin() < *R.begin() && *L.rbegin() < *R.rbegin()) {
            std::cout << "YES\n";
        } else {
            std::cout << "NO\n";
        }
    }

    return 0;
}

G

题意

给定一张图，\(q\) 次询问，每次给定一些边，求是否存在一个 MST（最小生成树）涵盖给定的所有边。

题解

考虑 Kruskal 求 MST 的性质，由于是从小到大加入边，所以考虑一条边时，已经将边权小于它的边都加入进去了。另一个性质是，每次选完小于或等于一个固定值的所有边后，图的连通性是固定的，如果有两种连通性 \(G_1,G_2\)，那么找出其中的不同，我们假定这个不同是在 \(G_1\) 中 \(u,v\) 连通，而在 \(G_2\) 中没有。那么将 \(G_2\) 的边试图加入 \(G_1\)，一定可以找到一条满足条件的边加入，说明还没有选完边。

因此，我们可以分别考虑每一种权值，并且在考虑每一种权值时，都认为比它小的权值都完成了 Kruskal 算法，具有一定的连通性。那么对于一次询问，我们从小到大处理，如果发生冲突（要加入的边已经连通），说明是不可能的。

我们用并查集维护连通性，由于分别考虑每一种权值，应该使用可撤销并查集。

时间复杂度：\(O(n \log n + k\log k)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

struct DSU {
    int n;
    std::vector<int> p, sz;
    std::vector<std::pair<int *, int>> stk;
    DSU() {}
    DSU(int n_) { init(n_); }
    void init(int n_) {
        n = n_;
        p.assign(n + 1, 0);
        iota(p.begin(), p.end(), 0);
        sz.assign(n + 1, 1);
        stk.clear();
    }
    int find(int x) {
        while (x != p[x]) {
            x = p[x];
        }
        return x;
    }

    void doit(int &x, int y) {
        stk.push_back({&x, x});
        x = y;
    }
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        if (sz[x] > sz[y]) {
            std::swap(x, y);
        }
        doit(sz[y], sz[y] + sz[x]);
        doit(p[x], y);
        return true;
    }
    void roll(int cnt) {
        while (stk.size() > cnt) {
            auto [x, y] = stk.back();
            stk.pop_back();
            *x = y;
        }
    }
};

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    std::vector<std::array<int, 4>> e(m + 1);
    for (int i = 1; i <= m; i++) {
        int x, y, w;
        std::cin >> x >> y >> w;
        e[i] = {w, x, y, i};
    }
    sort(e.begin() + 1, e.end());
    DSU dsu(n);

    std::vector<std::array<int, 2>> e2(m + 1);
    for (int i = 1, j; i <= m; i = j) {
        j = i;
        while (j <= m && e[j][0] == e[i][0]) {
            int id = e[j][3];
            e2[id][0] = dsu.find(e[j][1]);
            e2[id][1] = dsu.find(e[j][2]);
            j++;
        }
        while (i < j) {
            dsu.merge(e[i][1], e[i][2]);
            i++;
        }
    }

    dsu.init(n);
    sort(e.begin() + 1, e.end(), [&](auto &a, auto &b) { return a[3] < b[3]; });

    int q;
    std::cin >> q;
    while (q--) {
        int k;
        std::cin >> k;
        std::vector<std::array<int, 3>> tmp(k + 1);
        for (int i = 1; i <= k; i++) {
            int a;
            std::cin >> a;
            tmp[i] = {e[a][0], e2[a][0], e2[a][1]};
        }
        sort(tmp.begin() + 1, tmp.end());

        bool flag = true;
        for (int i = 1, j; i <= k; i = j) {
            int sz = dsu.stk.size();
            if (!dsu.merge(tmp[i][1], tmp[i][2])) {
                flag = false;
                break;
            }
            j = i + 1;
            while (j <= k && tmp[j][0] == tmp[i][0]) {
                if (!dsu.merge(tmp[j][1], tmp[j][2])) {
                    flag = false;
                    break;
                }
                j++;
            }
            dsu.roll(sz);
        }
        if (flag) {
            std::cout << "YES\n";
        } else {
            std::cout << "NO\n";
        }
    }

    return 0;
}

数论分块

数论分块是用来计算求和中含有除法向下取整的，如 \(\sum_{i = 1} ^ nf(i)g(\lfloor \frac{n}{i}\rfloor)\)。如果我们能快速计算出 \(f(i)\) 的前缀和（根据性质，或高级筛等），就能在 \(O(\sqrt{n})\) 的时间内计算这个求和。原理是，我们将满足等于 \(\lfloor \frac{n}{i}\rfloor\)​ 一起计算。

1
2
3
4
5
6
for (int l = 1, r; l <= n; l = r + 1) {
    	int q = n / l;
    	r = n / q;
  		// 前缀和乘 (n / l)
    	ans += (r - l + 1) * q;
    }

7 月 14 日 Round 5

哇，全是计数。rank 28 / 36，刚好被抓到软肋了，把这些计数补了希望能够提高吧。

B

题意

一棵无限大 \(n\) 叉树，每个节点都有 \(n\) 个儿子，距离分别为 \(d_1,...,d_n\)，求有多少个节点，到根节点的距离小于等于 \(x\)。

\(d_i\le 100, x\le 10^9\)

题解

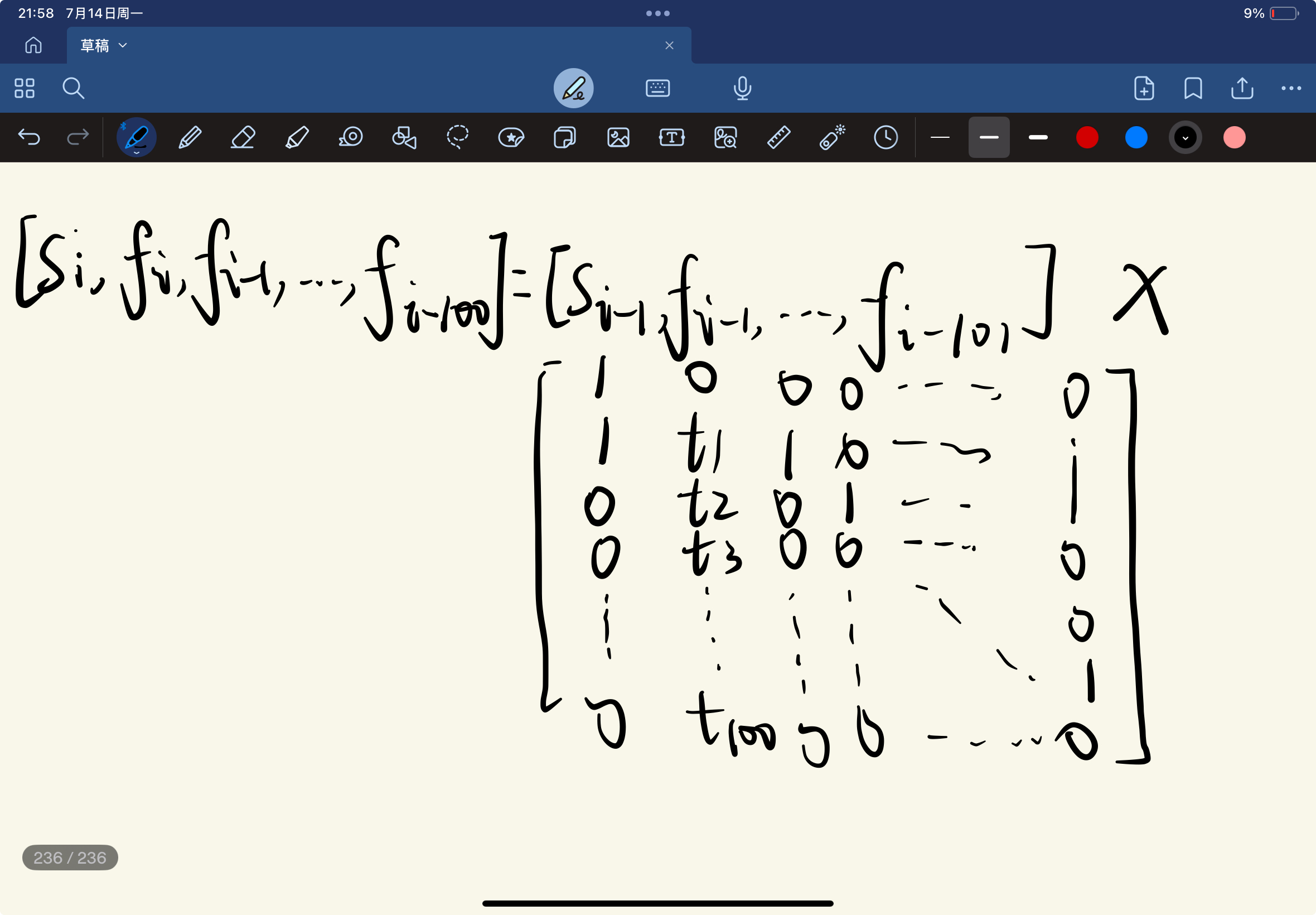
设 \(dp_i\) 为到根节点恰好距离为 \(i\) 的情况数，那么转移为 \(f_i = \sum_{j=1}^nf_{i-d_j}\)，复杂度是 \(O(nx)\) 的，无法通过。

考虑到 \(x\) 比较大，可以考虑矩阵加速。我们设 \(t_i\) 表示某个节点的儿子节点中，恰好有 \(t_i\) 个节点到它的距离为 \(i\)，那么转移方程还可以写为：\(f_i = \sum_{j=1}^{100}t_jf_{i-j}\)，这是线性递推，我们设 \(s_i = \sum_{j=1}^if_j\)，那么可以构造如下矩阵：

草稿 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1e9 + 7;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

std::vector<int> t(101);

struct Matrix {
    std::vector<std::vector<Z>> a;
    Matrix() { a.assign(102, std::vector<Z>(102)); }
    Matrix operator*(const Matrix &b) const {
        Matrix res;
        for (int i = 1; i <= 101; i++) {
            for (int j = 1; j <= 101; j++) {
                for (int k = 1; k <= 101; k++) {
                    res.a[i][j] += a[i][k] * b.a[k][j];
                }
            }
        }
        return res;
    }
    void inita() { a[1][1] = a[1][2] = 1; }
    void initb() {
        a[1][1] = 1;
        for (int i = 2; i <= 101; i++) {
            a[i][1] = a[i][2] = t[i - 1];
        }
        for (int i = 3; i <= 101; i++) {
            a[i - 1][i] = 1;
        }
    }
};

Matrix qpow(Matrix &a, int b) {
    Matrix res;
    for (int i = 1; i <= 101; i++) {
        res.a[i][i] = 1;
    }
    while (b) {
        if (b & 1) {
            res = res * a;
        }
        a = a * a;
        b /= 2;
    }
    return res;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, x;
    std::cin >> n >> x;
    std::vector<int> d(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> d[i];
        t[d[i]]++;
    }
    Matrix a, b;
    a.inita(), b.initb();
    b = qpow(b, x);
    a = a * b;

    std::cout << a.a[1][1] << "\n";

    return 0;
}

D

题意

将 1~n 的所有数作为一个排列，一共有 \(n!\) 个，将它们按照字典序拼接起来，求有多少个区间满足区间和为 \(\frac{n*(n+1)}{2}\)。

题解

显然满足条件的区间一定是长度为 \(n\) 的，且包含 1~\(n\) 所有数。那么，我们选择的区间，要么是每个排列，有 \(n!\) 个，要么要从两个连续的排列，前面取 \(k\) 个，后面取 \(n - k\) 个拼接起来。

考虑 std::next_permutaion 的实现方法：找出原排列的最长的单调递减的后缀，记长度为 \(k\)，然后在这个后缀中，找到比原排列第 \(n - k\) 个位置大的数（即后缀的前一个数），交换这两个位置，然后将新的后缀按照升序排序，等价于 reverse。这样，新生成的排列中，有 \(k + 1\) 个数的位置变化了，只有前面 \(n - k -1\) 个数保持原来的顺序。

假设对于前一个排列，我们要取 \(k\) 个数，那么后一个排列需要 \(n - k\) 个，如果这种取法合法，则后一个排列的前 \(n - k\) 位必须与前一个排列的 \(n - k\) 位相同，即这一段没有发生交换，因此，后缀长度 \(len\) 应该满足 \(len < k\)。

考虑用总方案数减去不合法的方案数，考虑对每一个排列，固定一个选择的个数 \(k\)，那么它不合法，当且仅当整个后缀就是单调降序的，因为此时会影响到前一个数，这样的排列共有 \(A_{n}^{n-k}\) 个。我们枚举每一个 \(k\)，而总共有 \(n\times n!\) 个数字，减去不合法的方案即为 \(n\times n! - \sum_{k=1}^{n-1}\frac{n!}{k!}\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 998244353;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    std::cin >> n;

    std::vector<Z> frac(2 * n + 1);
    frac[0] = 1;
    for (int i = 1; i <= 2 * n; i++) {
        frac[i] = frac[i - 1] * i;
    }

    Z ans = frac[n] * n;
    for (int i = 1; i <= n - 1; i++) {
        ans -= frac[n] / frac[i];
    }

    std::cout << ans << "\n";
    return 0;
}

E

题意

求从 $n $ 走到 1 的方案数：设当前位置为 \(x\) 可以减法，减去 \([1,x]\)，也可以除法，变为 \(\lfloor\frac{n}{i}\rfloor,i\in[2,x]\)。

题解

设 \(dp_i\) 为从 \(n\) 走到 \(i\) 的方案数，如果减法，就是 \(dp_i = \sum_{j= n}^{i+1}dp_j\)，如果除法，除以 2 的话，\(dp_i\) 由 \(dp_{2i},dp_{2i+1}\) 转移而来，除以 3 的话\(dp_i\) 由 \(dp_{3i},dp_{3i+1},dp_{3i+2}\) 转移过来...以此类推，除以 \(j\)，\(dp_i\) 由 \(dp_{ij}\)~\(dp_{ij+j-1}\) 转移过来。转移时维护后缀和，枚举除法的除数，复杂度为调和级数 \(O(n\log n)\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    D::setMod(m);
    std::vector<D> dp(n + 1);
    std::vector<D> suf(n + 2);
    dp[n] = suf[n] = 1;
    for (int i = n - 1; i >= 1; i--) {
        dp[i] += suf[i + 1];
        for (int j = 2; i * j <= n; j++) {
            dp[i] += suf[i * j] - suf[std::min(i * j + j, n + 1)];
        }
        suf[i] = suf[i + 1] + dp[i];
    }
    std::cout << dp[1] << "\n";

    return 0;
}

F

题意

给定 \(x,y\)，求有多少个数组 \(a\)，满足 \(\sum_{i=1}^n a_i = y\)，且 \(\gcd(a_1, a_2,...,a_n) = x\)。

题解

自然 \(y\pmod x \ne 0\) 时无解。

那么，先不考虑 \(gcd\) 的条件，问题转化为将 \(t = \frac{y}{x}\) 个 1 分成若干组。通过插板法应该有 \(\sum_{k=1}^{t}{\begin{pmatrix}t - 1\\k - 1\end{pmatrix}} = 2^{t-1}\)。

再考虑 \(gcd\) 的限制，我们可以枚举 \(t\) 的因数 \(d\) ，从总方案数减去它们对应的情况，这是相同的子问题，除此之外，也不能把所有数放在一起，再减去 1 即可。

值得注意的是，假设我们处理 \(t = 12\)，枚举 \(d = 2,3,6\)​​ 的情况应该是互相不重合的，不应该容斥。

时间复杂度：\(O(d(m)\sqrt{m}\log m)\)，\(d(m)\) 代表因数个数，不超过 \(O(\sqrt{m})\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1e9 + 7;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

std::map<int, Z> mp;

Z solve(int n) {
    if (n == 1) {
        return Z(1);
    }
    if (mp.count(n)) {
        return mp[n];
    }
    Z ans = power(Z(2), n - 1) - 1;
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            ans -= solve(i);
            if (i != n / i) {
                ans -= solve(n / i);
            }
        }
    }
    mp[n] = ans;
    return ans;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int x, y;
    std::cin >> x >> y;
    if (y % x) {
        std::cout << 0 << "\n";
        return 0;
    }
    std::cout << solve(y / x) << "\n";

    return 0;
}

还有莫比乌斯反演的做法：

我们设 \(f(x)\) 为答案，即有 \(x\) 个 1，拆成 \(\gcd = 1\) 的方案数。我们通过隔板法求出没有限制的情况下， \(g(x) = 2^{x - 1}\)，其实也就是 \(g(x) = \sum_{d\mid x}f(d)\)，考虑使用莫比乌斯反演，即 \(f(x) = \sum_{d\mid x}\mu(d)g(\frac{n}{d})\)。

暴力求解，时间复杂度：\(O(\sqrt{m})\)​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

constexpr int N = 1e7;
std::unordered_map<int, Z> fMu;
std::vector<int> minp, primes, phi, mu;
std::vector<i64> sphi;

void sieve(int n) {
    minp.assign(n + 1, 0);
    phi.assign(n + 1, 0);
    sphi.assign(n + 1, 0);
    mu.assign(n + 1, 0);
    primes.clear();
    phi[1] = 1;
    mu[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (minp[i] == 0) {
            minp[i] = i;
            phi[i] = i - 1;
            mu[i] = -1;
            primes.push_back(i);
        }
        for (auto p : primes) {
            if (i * p > n) {
                break;
            }
            minp[i * p] = p;
            if (p == minp[i]) {
                phi[i * p] = phi[i] * p;
                break;
            }
            phi[i * p] = phi[i] * (p - 1);
            mu[i * p] = -mu[i];
        }
    }
    for (int i = 1; i <= n; i++) {
        sphi[i] = sphi[i - 1] + phi[i];
        mu[i] += mu[i - 1];
    }
}

// 快速求 \sum_{i=1}^n \mu(i) 的杜教筛
Z sumMu(int n) {
    if (n <= N) {
        return mu[n];
    }
    if (fMu.count(n)) {
        return fMu[n];
    }
    if (n == 0) {
        return 0;
    }
    Z ans = 1;
    for (int l = 2, r; l <= n; l = r + 1) {
        r = n / (n / l);
        ans -= (r - l + 1) * sumMu(n / l);
    }
    fMu[n] = ans;
    return ans;
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    sieve(N);
    int x, y;
    std::cin >> x >> y;
    if (y % x) {
        std::cout << 0 << "\n";
        return 0;
    }
    Z ans = 0;
    int t = y / x;
    for (int i = 1; i * i <= t; i++) {
        if (t % i == 0) {
            ans += (sumMu(i) - sumMu(i - 1)) * power(Z(2), t / i - 1);
            if (t / i != i) {
                ans += (sumMu(t / i) - sumMu(t / i - 1)) * power(Z(2), i - 1);
            }
        }
    }
    std::cout << ans << "\n";

    return 0;
}

莫比乌斯反演

莫比乌斯函数的定义为： \[ \mu(n) = \left\{ \begin{array}{ll} 1 & \text{if } n = 1 \\ (-1)^k & \text{if } n \text{ 是 } k \text{ 个不同质数的乘积} \\ 0 & \text{if } n \text{ 有平方因子} \end{array} \right. \] 这是一个积性函数（对于 \(\gcd(x,y) = 1,f(x)f(y) = f(xy)\)），具有性质： \[ \sum_{d\mid n}\mu(d) = [n =1] \\\varphi(n) = \sum_{d\mid n}\mu(d)\frac{n}{d} \] 即 \(\mu* I = \epsilon,\mu * id = \varphi\)，其中 \(I\) 代表单位常量函数（\(I(x) = 1\)），\(id\) 代表恒等函数 （\(id(x) = x\)），“*” 代表狄利克雷卷积 \(h(n) = \sum_{d\mid n}f(d)g(\frac{n}{d})\)，记为 \((f*g)(n) = \sum_{d\mid n}f(d)g(\frac{n}{d})\)。

接下来，我们就可以定义莫比乌斯反演了，形象的说就是：莫比乌斯反演 = 用 Möbius 函数做“狄利克雷除法”。 \[ g(n) = \sum_{d\mid n}f(d) \iff f(n) = \sum_{d\mid n}\mu(d)g(\frac{n}{d}) \] 使用条件为：求和必须是整除形式。这样，我们已知 \(f(x)\) 之和 \(g(x)\)，可以通过莫比乌斯反演求出 \(f(x)\)。

例： \[ \begin{align*} &\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=1]\\\\ &=\sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid gcd(i,j)}\mu(d)\\\\ &=\sum_{i=1}^n\sum_{j=1}^m\sum_{d\mid i,d\mid j}\mu(d)\\\\ &=\sum_{d=1}^n\mu(d)\lfloor \frac{n}{d}\rfloor\lfloor \frac{m}{d}\rfloor \end{align*} \]

7 月 15 日 Round 6

rank 14 / 36。比较可惜的是跟榜导致没有开出来蛮多简单题，莫队想出来了但是因为一些性质没想到，写法上常数也出现了问题。只能说总算能稳定做到需要板子的题了。新学的：向上取整数论分块。

C

题意

给一个字符串 \(t\) 和一个整数 \(D\)，将 \(t\) 分成尽可能少的段，使得每一个段的周期不能超过 \(D\)，求最少分割段数。

题解

首先需要知道 KMP 中 前缀函数的一个结论：\(s\) 有长度为 \(r\) 的 border，则 \(\mid s\mid - r\) 是 \(s\) 的周期。我们可以一段一段 KMP 处理，每当遇到 \(\mid s\mid - r > D\) 时，就在当前位置停止 KMP，前一个位置就是上一段的终点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    std::string s;
    std::cin >> s;
    int D;
    std::cin >> D;

    int n = s.size();
    s = " " + s;
    auto kmp = [&](const std::string &s) {
        std::vector<int> fail(n + 1);
        fail[0] = fail[1] = 0;
        for (int i = 2, j = 0; i <= n; i++) {
            while (j && s[j + 1] != s[i]) {
                j = fail[j];
            }
            if (s[j + 1] == s[i]) {
                j++;
            }
            fail[i] = j;
            if (i - fail[i] > D) {
                return i - 1;
            }
        }
        return n + 1;
    };
    int ans = 0;
    for (int i = 1; i <= n;) {
        ans++;
        int ed = kmp(s.substr(i - 1));
        i += ed;
    }
    std::cout << ans << "\n";

    return 0;
}

E

题意

给一张连通图和起点、终点，有一些特殊边。求起点到终点的路径中，是否能经过特殊边，每条边只能走一次。

题解

边双连通分量缩点即可，缩成一棵树之后，只需要判断简单路径中是否存在这样的边，将存在特殊边的边双标记，枚举路径上所有边判断是否有标记。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

struct EDCC {
    int n, now, cnt;
    std::vector<std::vector<std::array<int, 2>>> ver;
    std::vector<int> dfn, low, bel, S;
    EDCC(int n) : n(n), ver(n + 1), low(n + 1) {
        dfn.resize(n + 1, -1);
        bel.resize(n + 1, -1);
        now = cnt = 0;
    }
    void add(int x, int y, int z) {
        ver[x].push_back({y, z});
        ver[y].push_back({x, z});
    }
    void tarjan(int x, int fa) {
        dfn[x] = low[x] = now++;
        S.push_back(x);
        for (auto [y, w] : ver[x]) {
            if (y == fa) {
                continue;
            }
            if (dfn[y] == -1) {
                tarjan(y, x);
                low[x] = std::min(low[x], low[y]);
            } else {
                low[x] = std::min(low[x], dfn[y]);
            }
        }
        if (dfn[x] == low[x]) {
            int pre;
            cnt++;
            do {
                pre = S.back();
                bel[pre] = cnt;
                S.pop_back();
            } while (pre != x);
        }
    }
    auto work() {
        for (int i = 1; i <= n; i++) {
            if (dfn[i] == -1) {
                tarjan(i, 0);
            }
        }
        std::vector<int> siz(cnt + 1);
        std::vector<std::vector<std::array<int, 2>>> adj(cnt + 1);
        for (int i = 1; i <= n; i++) {
            siz[bel[i]]++;
            for (auto [j, w] : ver[i]) {
                int x = bel[i], y = bel[j];
                if (x != y) {
                    adj[x].push_back({y, w});
                }
            }
        }
        return std::tuple{cnt, adj, bel, siz};
    }
};

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    EDCC edcc(n);
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        std::cin >> x >> y >> z;
        edcc.add(x, y, z);
    }
    int a, b;
    std::cin >> a >> b;
    auto [cnt, adj, bel, siz] = edcc.work();
    std::vector<int> p(n + 1);
    auto dfs = [&](auto dfs, int x, int fa) -> void {
        p[x] = fa;
        for (auto [y, _] : adj[x]) {
            if (y == fa) {
                continue;
            }
            dfs(dfs, y, x);
        }
    };
    dfs(dfs, bel[a], 0);

    int cur = bel[b];
    std::vector<bool> vis(cnt + 1);
    while (cur != bel[a]) {
        vis[cur] = true;
        cur = p[cur];
    }
    vis[bel[a]] = true;

    for (int x = 1; x <= n; x++) {
        for (auto [y, w] : edcc.ver[x]) {
            if (vis[bel[x]] && vis[bel[y]] && w == 1) {
                std::cout << "YES\n";
                return 0;
            }
        }
    }
    std::cout << "NO\n";

    return 0;
}

H

题意

给定一个矩阵，寻找一条路径，上升的次数 \(\le\) 下降的次数。

题解

榜歪了，漏掉的签到啊。

随便找一条路径，正向不行反向就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    std::cin >> n;
    std::vector<std::vector<int>> a(n + 1, std::vector<int>(n + 1));
    std::vector<int> b;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            std::cin >> a[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        if (i & 1) {
            for (int j = 1; j <= n; j++) {
                b.push_back(a[i][j]);
            }
        } else {
            for (int j = n; j >= 1; j--) {
                b.push_back(a[i][j]);
            }
        }
    }
    int up = 0, down = 0;
    for (int i = 0; i < b.size() - 1; i++) {
        up += b[i] < b[i + 1];
        down += b[i] > b[i + 1];
    }
    if (up > down) {
        reverse(b.begin(), b.end());
    }
    for (int i = 0; i < b.size(); i++) {
        std::cout << b[i] << " \n"[i == b.size() - 1];
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

I

题意

给定一个长为 \(n\) 的序列 \(a\)，\(q\) 次询问，每次选择一个区间 \([l, r]\) ，选择一个数 \(p > 1\)，使得 \(p\) 整除区间内尽可能多的数，求最多能整除多少个数。

\(n\le 5\times 10^4,a_i\le 10^6\)。

题解

想到莫队了，但是性质没有想完整。我们对于每个数可以求出所有因数，对于单轮询问，遍历区间内所有数的因数，记 \(mp_x\) 为因数为 \(x\) 可以整除的数字的数量，\(cnt_x\) 为能整除 \(x\) 的数的因数的个数，方便我们统计答案。

但是因数还是比较多，上面的做法是 \(O(n\sqrt{A}d(A))\) 的，因数个数还是有 \(O(\sqrt{A})\) 的级别，会近似 \(O(n^2)\)。一个观察是，只需要考虑因数为素数的情况，因为假设合数能够作为答案，它的质因数一定更优。那么，根据素数分布，复杂度是 \(O(n\sqrt{A}\frac{d(A)}{\ln n})\) 的。

注意多测，不能每次都在 solve() 函数里开 \(cnt\) 和 \(mp\)，而这两个数组又是固定长度的，也不能单次清空。一个做法是，根据莫队的性质，我们在一组询问结束后将指针移动至 \(l > r\)，就能清空这两个数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

constexpr int N = 1e6 + 1;
constexpr int M = 5e4 + 1;
std::vector<int> nums[N];
int cnt[N], mp[N];
int st[M], ed[M], bel[M];
int res[M];

// minp(x) 可以找到 x 大于 1 的最小质因子
std::vector<int> minp, primes;
void sieve(int n) {
    minp.assign(n + 1, 0);
    primes.clear();
    for (int i = 2; i <= n; i++) {
        if (minp[i] == 0) {
            minp[i] = i;
            primes.push_back(i);
        }
        for (auto p : primes) {
            if (i * p > n) {
                break;
            }
            minp[i * p] = p;
            if (p == minp[i]) {
                break;
            }
        }
    }
}

void get(int x) {
    if (nums[x].size()) {
        return;
    }
    int y = x;
    for (int i = 0; primes[i] * primes[i] <= x; i++) {
        if (x % primes[i] == 0) {
            nums[y].push_back(primes[i]);
            while (x % primes[i] == 0) {
                x /= primes[i];
            }
        }
    }
    if (x != 1) {
        nums[y].push_back(x);
    }
};

void solve() {
    int n, q;
    std::cin >> n >> q;
    std::vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        get(a[i]);
    }
    int sqn = sqrt(n);
    for (int i = 1; i <= sqn; i++) {
        st[i] = n / sqn * (i - 1) + 1;
        ed[i] = n / sqn * i;
    }
    ed[sqn] = n;
    for (int i = 1; i <= sqn; i++) {
        for (int j = st[i]; j <= ed[i]; j++) {
            bel[j] = i;
        }
    }
    std::vector<std::array<int, 3>> e(q + 1);
    for (int i = 1; i <= q; i++) {
        int x, y;
        std::cin >> x >> y;
        e[i] = {x, y, i};
    }
    std::sort(e.begin() + 1, e.end(), [&](auto &a, auto &b) {
        if (bel[a[0]] == bel[b[0]]) {
            return bel[a[0]] % 2 == 1 ? a[1] < b[1] : a[1] > b[1];
        }
        return a[0] < b[0];
    });
    int l = 0, r = -1;
    int ans = 0;
    auto add = [&](int x) {
        if (x == 0 || a[x] == 1) {
            return;
        }
        for (auto y : nums[a[x]]) {
            mp[cnt[y]]--;
            cnt[y]++;
            mp[cnt[y]]++;
            ans = std::max(ans, cnt[y]);
        }
    };
    auto del = [&](int x) {
        if (x == 0 || a[x] == 1) {
            return;
        }
        for (auto y : nums[a[x]]) {
            mp[cnt[y]]--;
            if (mp[cnt[y]] == 0 && ans == cnt[y]) {
                ans--;
            }
            cnt[y]--;
            mp[cnt[y]]++;
        }
    };
    for (int i = 1; i <= q; i++) {
        auto [x, y, id] = e[i];
        while (l > x) {
            add(--l);
        }
        while (r < y) {
            add(++r);
        }
        while (l < x) {
            del(l++);
        }
        while (r > y) {
            del(r--);
        }
        res[id] = ans;
    }
    for (int i = 1; i <= q; i++) {
        std::cout << res[i] << "\n";
    }
    while (l <= r) {
        del(l++);
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    sieve(1e6);
    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

J

题意

给定 \(n,m\)，每次操作可以将 \(n\) 减 1 或将 \(m\) 加 1，求进行多少次操作能够让 \(n\mid m\)。

\(n,m\le 10^8\)。

题解

存在多测，时间复杂度只能是 \(O(T\sqrt{n})\)​ 的，尝试打过表，不存在规律，还是老实推导吧。

由于 \(n\) 是因数，要小一些，从 \(n\) 出发会比较好。设 \(n\) 变成 \(n^\prime\)，那么恰好能够满足条件的 \(m^\prime = \lceil\frac{m}{n^\prime}\rceil\times n^\prime\)，因此答案就是 \((n - n^\prime) + (\lceil\frac{m}{n^\prime}\rceil n^\prime - m) = (\lceil\frac{m}{n^\prime}\rceil - 1)n^\prime + n - m\)，由于 \(\lceil\frac{m}{n^\prime}\rceil\) 的取值只有根号个，我们可以考虑枚举，通过数论分块，将取值等于 \(\lceil\frac{m}{x}\rceil\) 的所有 \([l,r]\) 一起计算，由于我们只需要最小值，取 \(n^\prime = l\) 即可。这里需要向上取整的数论分块。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n, m;
    std::cin >> n >> m;
    int ans = 2e9;
    for (int l = 1, r; l <= n; l = r + 1) {
        int k = (m + l - 1) / l;
        r = (k == 1) ? n : (m - 1) / (k - 1);
        // 区间 [l, r] \in [1, n] 内，所有 ceil(m / i) 的值都等于 k
        ans = std::min(ans, (k - 1) * l + n - m);
    }
    std::cout << ans << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

7 月 16 日 Round 7

唉唉唉，一方面忘了三小时场是按难度顺序排序了，开局倒开 F 题，瞪了 10 分钟一看榜过了十几个 A 了才反应过来。然后 C 题可惜了，大致是想出来了，细节出了点问题，不加排序规则，让它自己从小到大排序就过了qwq。

rank 反而变高了，原来今天查违规了，喜提最近四次队内赛白忙活...

一看原来没多少训练赛了呀，之后一定要更努力把 rank 提上去。

C

题意

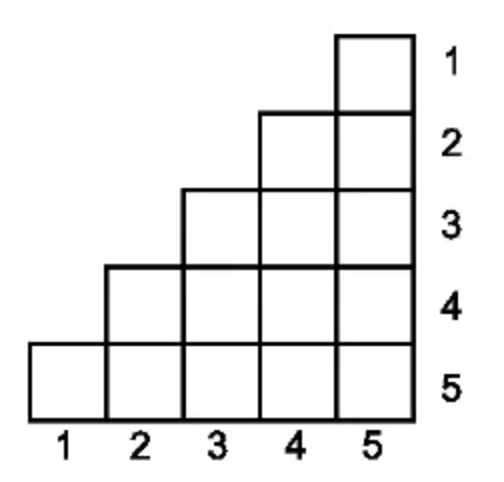
有一个 \(n\times n\) 的方阵，副对角线（左下—右上）的左上方被去掉了，如图所示。

image-20250716201019094

方阵中有 \(m\) 个人，每个人在一秒内可以走到相邻的一个格子。在开始前，他们可以分别选择一条到副对角线的最短路径。然后他们同时开始沿着最短路径运动，走到副对角线上时停止。在任何时刻，两个人不能位于同一个格子（即使他们已经停止运动）。

请保留最多的人，使得存在一种合法的移动方案。

\(n,m\le 10^5\)

题解

考虑怎么才会碰撞，由于每秒所有人都在移动，因此可能碰撞的只有在同一条副对角线上的。可以发现每一块能覆盖到的终点是可以求出来了，现在问题就变成了，每个人都能覆盖某个区间，但是只能到区间内的一个位置，要让到终点的人最多，且同一个副对角线的不能发生碰撞。

要使得不发生碰撞，我们考虑给每一个人找不同的终点，我们可以必须先填充左边的区间，再填充右边的就可以了。

因此，我们只需要从一端开始处理，不妨枚举每个位置是否能被放，用单调队列加入每个区间，如果有满足位置的区间，贪心放就行。

时间复杂度：\(O(n\log m)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    std::vector<int> l(m + 1), r(m + 1);
    std::vector<std::vector<int>> f(n + 1);
    for (int i = 1; i <= m; i++) {
        std::cin >> l[i] >> r[i];
        l[i] = n - l[i] + 1;
        f[l[i]].push_back(i);
    }
    std::priority_queue<std::array<int, 2>, std::vector<std::array<int, 2>>,
                        std::greater<>>
        pq;
    std::vector<int> ans;
    for (int i = 1; i <= n; i++) {
        for (auto j : f[i]) {
            pq.push({r[j], j});
        }
        while (!pq.empty()) {
            auto [r, j] = pq.top();
            pq.pop();
            if (r < i) {
                continue;
            }
            ans.push_back(j);
            break;
        }
    }
    std::cout << ans.size() << "\n";
    for (int i = 0; i < ans.size(); i++) {
        std::cout << ans[i] << " \n"[i == ans.size() - 1];
    }

    return 0;
}

还有我赛时的唐诗做法，不过排序自定义规则反而错了，我是用 std::set 一开始存所有数的，然后 lower_bound 找第一个满足条件的数，但是我不知道我怎么想的，按右端点排序...

时间复杂度：\(O((n + m)\log n)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    std::vector<std::array<int, 4>> a(m + 1);
    for (int i = 1; i <= m; i++) {
        int x, y;
        std::cin >> x >> y;
        a[i] = {y, x, x + y, i};
    }
    sort(a.begin() + 1, a.end());
    std::vector<int> ans;
    int cnt = n;
    int mx = n;
    std::set<int> st;
    for (int i = 1; i <= n; i++) {
        st.insert(i);
    }
    for (int i = 1; i <= m; i++) {
        auto [y, x, s, id] = a[i];
        int l = n - x + 1, r = y;
        auto it = st.lower_bound(l);
        if (it == st.end() || *it > r) {
            continue;
        }
        ans.push_back(id);
        st.erase(it);
    }
    std::cout << ans.size() << "\n";
    for (int i = 0; i < ans.size(); i++) {
        std::cout << ans[i] << " \n"[i == ans.size() - 1];
    }

    return 0;
}

D

题意

给定一个数组 \(a\)，\(q\) 次询问，每次给定一个区间 \([l,r]\) 求这个区间内 \((t_1,...,t_k)\) 的数量，满足 \(l\le t_1<t_2<...<t_k\le r\) 且 \(a_{t_i}\mid a_{t+1}\)。

题解

考虑单次询问整个区间，对于计数，我们可以想到 dp，设 \(f_{i,k}\) 为区间 \([i,k]\) 的答案，那么转移为 \(f_{i,k} = \sum_{i\le j\le k}dp_{j,k}[a_j\mid a_k]\)，由于存在整除的条件，如果固定左端点 \(l\) ，我们可以枚举 \(a_l\) 的倍数的位置作为 \(j\) 和 \(k\)，做到均摊 \(O(\log^2 n)\) 级别的转移。

多次询问可以离线处理，考虑怎么才能利用之前的答案，我们从右往左处理各个左端点开头的区间，对于处理的左端点 \(i\)，考虑对 \(i < j\) 的贡献，我们在 \(dp\) 转移时可以将 \(i\) 右边的位置的贡献挂在 \(j\)​ 上，我们通过树状数组维护区间和，就能快速查询一个区间的总贡献。

时间复杂度：\(O(n\log^2n)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

struct Fenwick {
    int n;
    std::vector<i64> a;
    Fenwick(int n = 0) { init(n); }
    void init(int n_) {
        n = n_;
        a.assign(n_ + 1, 0);
    }
    void add(int x, i64 v) {
        for (int i = x; i <= n; i += i & -i) {
            a[i] += v;
        }
    }
    i64 sum(int x) {
        i64 res = 0;
        for (int i = x; i >= 1; i -= i & -i) {
            res += a[i];
        }
        return res;
    }
    i64 rangeSum(int l, int r) { return sum(r) - sum(l - 1); }
};

void solve() {
    int n, q;
    std::cin >> n >> q;
    std::vector<int> a(n + 1), pos(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        pos[a[i]] = i;
    }
    std::vector<std::vector<int>> r(n + 1), e(n + 1);
    for (int i = 1; i <= q; i++) {
        int x, y;
        std::cin >> x >> y;
        r[x].push_back(y);
        e[x].push_back(i);
    }
    std::vector<int> dp(n + 1);
    Fenwick bit(n);
    std::vector<int> ans(q + 1);
    for (int i = n; i >= 1; i--) {
        int x = a[i];
        dp[x] = 1;
        for (int y = x; y <= n; y += x) {
            if (pos[y] < pos[x]) {
                continue;
            }
            for (int z = y * 2; z <= n; z += y) {
                if (pos[z] < pos[y]) {
                    continue;
                }
                dp[z] += dp[y];
            }
        }
        for (int j = x; j <= n; j += x) {
            bit.add(pos[j], dp[j]);
            dp[j] = 0;
        }
        for (int j = 0; j < r[i].size(); j++) {
            ans[e[i][j]] += bit.rangeSum(i, r[i][j]);
        }
    }
    for (int i = 1; i <= q; i++) {
        std::cout << ans[i] << " \n"[i == q];
    }
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

7 月 17 日 Round 8

怎么越来越菜了。rank 30 / 36。Round 已经过半了，接下去必须要发力了啊啊啊啊。

算是纠正了字符串板子的用法吧，不过为什么这几天老是看不出性质啊啊啊啊啊

A

题意

\(n\) 辆车，\(m\) 对关系，每辆车至少在一种关系中，包括两辆车一定相遇或一定不会相遇。构造一种情况，规定车的方向和位置，使得关系成立或判断不可能。

题解

一定相遇，则二者相向运动，左边的车往右且右边的车往左；一定不相遇，则二者相离运动，左边的车往左且右边的车往右。

那么，只要两辆车有关系，他们的方向一定相反，我们在这两辆车连边，则最后会构成一张二分图，可以判断是否存在二分图。

如果存在，那么我们不妨重新连边，由左边的车向右边的连边，会形成拓扑序，我们先判定是否存在环，不存在的话按照拓扑序赋值即可。

时间复杂度：\(O(n+m)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int>> adj(n + 1);
    std::vector<std::vector<std::array<int, 2>>> e(3);
    for (int i = 1; i <= m; i++) {
        int op, x, y;
        std::cin >> op >> x >> y;
        adj[x].push_back(y);
        adj[y].push_back(x);
        e[op].push_back({x, y});
    }
    std::queue<int> q;
    std::vector<int> f(n + 1, -1);
    bool ok = true;
    for (int i = 1; i <= n; i++) {
        if (f[i] == -1) {
            q.push(i);
            f[i] = 0;
            while (!q.empty()) {
                int x = q.front();
                q.pop();
                for (auto y : adj[x]) {
                    if (f[y] == -1) {
                        f[y] = f[x] ^ 1;
                        q.push(y);
                    } else if (f[x] == f[y]) {
                        ok = false;
                        break;
                    }
                }
            }
        }
    }
    if (!ok) {
        std::cout << "NO\n";
        return 0;
    }
    for (int i = 1; i <= n; i++) {
        adj[i].clear();
    }
    std::vector<int> deg(n + 1);
    for (auto [x, y] : e[1]) {
        if (f[x] == 0) {
            adj[x].push_back(y);
            deg[y]++;
        } else {
            adj[y].push_back(x);
            deg[x]++;
        }
    }
    for (auto [x, y] : e[2]) {
        if (f[x] == 1) {
            adj[x].push_back(y);
            deg[y]++;
        } else {
            adj[y].push_back(x);
            deg[x]++;
        }
    }
    std::vector<bool> vis(n + 1);
    std::vector<bool> ins(n + 1);
    for (int i = 1; i <= n; i++) {
        if (deg[i] == 0) {
            auto dfs = [&](auto dfs, int x) {
                ins[x] = true;
                vis[x] = true;
                bool res = true;
                for (auto y : adj[x]) {
                    if (ins[y]) {
                        return false;
                    }
                    if (!vis[y]) {
                        res &= dfs(dfs, y);
                    }
                }
                ins[x] = false;
                return res;
            };
            if (!dfs(dfs, i)) {
                std::cout << "NO\n";
                return 0;
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        if (!vis[i]) {
            std::cout << "NO\n";
            return 0;
        }
    }
    while (!q.empty()) {
        q.pop();
    }
    for (int i = 1; i <= n; i++) {
        if (deg[i] == 0) {
            q.push(i);
        }
    }
    int t = -1e9;
    std::vector<int> ans(n + 1);
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        ans[x] = t++;
        for (auto y : adj[x]) {
            deg[y]--;
            if (deg[y] == 0) {
                q.push(y);
            }
        }
    }
    std::cout << "YES\n";
    for (int i = 1; i <= n; i++) {
        if (f[i] == 0) {
            std::cout << "L ";
        } else {
            std::cout << "R ";
        }
        std::cout << ans[i] << "\n";
    }

    return 0;
}

E

题意

\(n\) 个硬币，每个有价值 \(c_i\)，选出一个子集，总价值为 \(k\)，再在这个子集里面选一些硬币，求可能的价值。

\(n,c,k\le 500\)

题解

英文题面非常绕，读懂之后发现 dp 就行，且这个数据范围一般都是 dp。设 \(dp_{i,j,k}\) 为前 \(i\) 个硬币，选出总价值为 \(j\)，其中一个子集价值为 \(k\) 是否可行。可以压缩一维，初始状态 \(dp_{0,0} = true\)，转移就是枚举当前数加不加入子集，如果加入，还加不加入子集的子集，也就是 \(dp_{i,j} = dp_{i,j}\mid dp_{i-a[i],j}\mid dp_{i-a[i],j-a[i]}\)​。

时间复杂度：\(O(n^3)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k;
    std::cin >> n >> k;
    std::vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
    }
    std::vector<std::vector<int>> dp(k + 1, std::vector<int>(k + 1));
    dp[0][0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = k; j >= a[i]; j--) {
            for (int p = k; p >= 0; p--) {
                if (p >= a[i]) {
                    dp[j][p] |= dp[j - a[i]][p - a[i]];
                }
                dp[j][p] |= dp[j - a[i]][p];
            }
        }
    }
    std::vector<int> ans;
    for (int i = 0; i <= k; i++) {
        if (dp[k][i]) {
            ans.push_back(i);
        }
    }
    std::cout << ans.size() << "\n";
    for (int i = 0; i < ans.size(); i++) {
        std::cout << ans[i] << " \n"[i == ans.size() - 1];
    }

    return 0;
}

G

题意

设 \(f(x)\) 表示第一个不整除 \(x\) 的数，求 \(\sum_{i=1}^nf(i)\)。

\(n\le 10^{16}\)

题解

多思考性质啊喂，别上来就打表找规律了！！！！！！

考虑 \(f(i)\) 怎么取值，最小是 2，如果要取 3 的话，2 就要整除 \(i\)，同理，如果 \(f(i) = x\)，1 到 \(x - 1\) 的所有数都要整除 \(i\)，即 \(\text{lcm}(1,2,...,x-1) \mid i\)。事实上，\(\text{lcm}(1,2,...,41) > 10^{18}\)，因此我们可以直接枚举答案为 1, 2, ..., 41。

假设正在枚举 \(x\)，那么满足条件的数被 \(\text{lcm}(1,2,...,x-1)\) 整除，又不被 \(\text{lcm}(1,2,...,x)\) 整除，根据容斥原理计算即可。

时间复杂度：\(O(T)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

i64 gcd(i64 x, i64 y) { return y == 0 ? x : gcd(y, x % y); }

i64 lcm(i64 x, i64 y) { return x / std::gcd(x, y) * y; }

void solve() {
    i64 n;
    std::cin >> n;
    i64 mul = 1;
    Z ans = 0;
    for (int i = 2; i <= 41; i++) {
        ans += 1ll * (n / mul - n / (lcm(mul, i))) * i;
        mul = lcm(mul, i);
    }
    std::cout << ans << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

7 月 18 日 Round 9

可惜啊，可惜啊啊啊啊啊。rank 22 / 36，要进不了队了呜呜呜呜😭不多说了还是补题吧。

C

题意

初始给定 \(n\) 个数在集合中，然后按如下规则拓展这个无限大的集合：如果 \(y\) 在集合中，将 \(2y+1\) 和 \(4y\) 也加入。求集合中大小小于 \(2^p\) 的数有多少个。

题解

思考：为什么是 \(2^p\) 呢。小于 \(2^p\) 的数，说明在二进制下位数最多为 \(p\) 位，那么对于两个操作我们也可以解释了：\(2y + 1\) 就是在 \(y\) 的二进制表示后面增加一个 1，\(4y\) 就是在 \(y\) 的二进制表示后面增加两个 0，容易发现这两个操作形成的数也是不同的。

考虑将每一个数拓展到 \(p\) 位的答案，那么新增加的个数是 \(dp_{i-1} + dp_{i-2}\)，是一个斐波那契数列，并且有结论：\(\sum_{i=1}^nfib(i) = fib(i + 2) - 1\)。我们只需要知道可拓展的位数即可求出答案。

接下来就只需要考虑重复的情况了，如果两个数能新增的数有重合，那么他们一定有相同的前缀，且多出来的后缀可以通过上述操作得到。那么我们排序后依次计算，每枚举到一个数时，先考虑是否有这样的情况，否则加上斐波那契数列的和即可。

注意：std::__lg(x) 函数返回二进制下最高位的指数，因此一个数的二进制位数是 __lg(x) + 1（该函数对 0 使用返回 -1）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, p;
    std::cin >> n >> p;
    std::map<int, int> mp;
    std::vector<Z> dp(p + 3);
    dp[0] = dp[1] = 1;
    for (int i = 2; i <= p + 2; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    Z ans = 0;
    std::vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
    }
    sort(a.begin() + 1, a.end());
    for (int i = 1; i <= n; i++) {
        int x = a[i];
        auto check = [&](int x) {
            while (x) {
                if (mp.count(x)) {
                    return false;
                } else if (x & 1) {
                    x /= 2;
                } else if (x & 2) {
                    break;
                } else {
                    x /= 4;
                }
            }
            return true;
        };
        if (check(x) && p + 2 >= std::__lg(x) + 1) {
            mp[x] = 1;
            ans += dp[p - std::__lg(x) + 1] - 1;
        }
    }
    std::cout << ans << "\n";

    return 0;
}

D

题意

给定一张图和图中两点 \(a,b\)，求有多少点对 \((p,q)\)，从 \(p\) 到 \(q\) 的路径上一定会经过 \(a,b\)。

题解

显然 \(a,b\) 要作为割点， \(a,b\) 中间的点都不满足题意，满足题意的点只有不经过 \(a\) 不能到达 \(b\) 的和不经过 \(b\) 不能到达 \(a\) 的。通过两次 DFS 即可求出，二者相乘即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n, m, a, b;
    std::cin >> n >> m >> a >> b;
    std::vector<std::vector<int>> adj(n + 1);
    for (int i = 1; i <= m; i++) {
        int x, y;
        std::cin >> x >> y;
        adj[x].push_back(y);
        adj[y].push_back(x);
    }
    std::vector<bool> vis(n + 1);
    auto dfs = [&](auto dfs, int x, int b) -> void {
        vis[x] = true;
        for (auto y : adj[x]) {
            if (vis[y] || y == b) {
                continue;
            }
            dfs(dfs, y, b);
        }
    };
    dfs(dfs, a, b);
    int cntb = -1;
    for (int i = 1; i <= n; i++) {
        cntb += vis[i] == false;
    }
    vis.assign(n + 1, false);
    dfs(dfs, b, a);
    int cnta = -1;
    for (int i = 1; i <= n; i++) {
        cnta += vis[i] == false;
    }
    std::cout << 1ll * cnta * cntb << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

E

题意

交互题。

在 \([1,1]\) 到 \([10^9,10^9]\) 的正方形区域内，40 次询问找到一个矩形。可以询问一个坐标，回答矩形离坐标的最近曼哈顿距离。

题解

这种矩形的交互套路就是问边界解方程。如果我们询问 $(1,1) $ 到 \((1,10^9)\) 可以发现，回答的值是先递减后递增的，且中间区域是相等的。那么我们询问两端，求中心点就可以知道矩形上边界到原图上边界的距离，然后再询问另一个角上的点，即可解方程。

只需要 4 次询问。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    auto query = [&](int x, int y) {
        std::cout << "? " << x << " " << y << std::endl;
        int d;
        std::cin >> d;
        return d;
    };
    auto answer = [&](int x, int y, int p, int q) {
        std::cout << "! " << x << " " << y << " " << p << " " << q << std::endl;
    };
    constexpr int inf = 1e9;
    int d1 = query(1, 1), d2 = query(1, inf), d3 = query(inf, 1);
    int u = query(1, (1 + inf - d2 + d1) / 2);
    int l = d1 - u, r = d2 - u, d = d3 - l;
    answer(1 + u, 1 + l, inf - d, inf - r);

    return 0;
}

7 月 19 日 Round 10

rank 17。最累的一天，因为还有 ABC 和 Div1 + 2，20 日虽然休息，不过晚上有 ARC（Div. 1），比赛太频繁了还要写几何专题就暂时没补题 qwq

7 月 21 日 Round 11

rank 11。不容易，今天没怎么吃罚时，但是中档题还是得加强。最后一周了，再接再厉。

E

题意

给定一张无重边，有向图，由较小值连向较大值，求路径序列的长度的最大值，满足序列中每一条路径，至少有一条边与前面的所有边都不相同。

题解

由于图的有向性，对于一条有向边 \((u, v)\)，如果 1 不能到达 \(u\)，或 \(v\) 不能到达 \(n\)，这条边就没有作用，我们考虑建立一张新图，有 \(N\) 个点，\(M\) 条边，且每个点都存在从 1 到达 \(n\) 的路径。

考虑在序列 \(\{p_1,p_2,...,p_{i - 1}\}\) 中新增一个序列 \(p_i\)，由于没有重边，如果 \(p_i\) 经过了 \(k_i\) 个之前从未经过的点（除了起点、终点），那么就会新增至少 \(k_i + 1\) 条从未经过的边，我们想让答案最大，因此只增加 \(k_i + 1\) 条边。

设答案为 \(x\)，有 \(\sum_{i=1}^xk_i = N - 2, \sum_{i=1}^x(k_i + 1) = \sum_{i=1}^xk_i + x = M\)。

那么，\(x = M - N + 2\)​​。

时间复杂度：\(O(n+m)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int>> adj(n + 1), rev(n + 1);
    for (int i = 1; i <= m; i++) {
        int x, y;
        std::cin >> x >> y;
        if (x > y) {
            std::swap(x, y);
        }
        adj[x].push_back(y);
        rev[y].push_back(x);
    }
    std::vector<int> f(n + 1), g(n + 1);
    auto dfs = [&](auto dfs, int x) -> void {
        f[x] = true;
        for (auto y : adj[x]) {
            if (f[y]) {
                continue;
            }
            dfs(dfs, y);
        }
    };
    dfs(dfs, 1);

    if (f[n] == false) {
        std::cout << 0 << "\n";
        return 0;
    }

    auto dfs2 = [&](auto dfs2, int x) -> void {
        g[x] = true;
        for (auto y : rev[x]) {
            if (g[y]) {
                continue;
            }
            dfs2(dfs2, y);
        }
    };
    dfs2(dfs2, n);

    int N = 0, M = 0;
    for (int i = 1; i <= n; i++) {
        if (f[i] && g[i]) {
            N++;
            for (auto j : adj[i]) {
                M += f[j] && g[j];
            }
        }
    }

    std::cout << M - N + 2 << "\n";

    return 0;
}

F

题意

给定 \(n\) 个球，其中前 \(k\) 个是特殊球，每个球都有权值。Alice 和 Bob 轮流拿球，Alice 先手行动，如果一个人拿到特殊球，可以再拿一次。求两人获得分值的期望。

题解

拿到特殊球不改变行动的人，那么我们可以在 \(n - k\) 个普通球形成的 \(n - k + 1\) 个间隔中放入特殊球，可以认为取到某个特殊球，就把那个间隔所有间隔的球都取走。同时，我们还可以认为普通球和特殊球的操作独立互不影响。

设 \(sum_1 = \sum_{i=1}^kv_i,sum_2 = \sum_{i=k + 1}^nv_i\)，对于特殊球，Alice 会拿 \(\lceil \frac{n-k+1}{2}\rceil\) 个间隔，每个间隔的特殊球个数期望是 \(\frac{k}{n-k+1}\)，那么从特殊球得到的分数就是 \(sum_1\times \lceil \frac{n-k+1}{2}\rceil \times\frac{k}{n-k+1}\)，对于普通球，两个人轮流拿，Alice 会拿 \(\lceil \frac{n-k}{2}\rceil\) 个间隔，得到的分数是 \(\lceil \frac{n-k}{2}\rceil\times sum_2\)，两者相加就是 Alice 的期望。Bob 的期望用总和减去 Alice 的期望即可。注意特判 \(n = k\) 的情况。

时间复杂度：\(O(\log\omega)\) ，求逆元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

void solve() {
    int n, k;
    std::cin >> n >> k;
    std::vector<int> a(n + 1);
    Z sum1, sum2 = 0;
    Z all = 0;
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        if (i <= k) {
            sum1 += a[i];
        } else {
            sum2 += a[i];
        }
        all += a[i];
    }
    if (n == k) {
        sum1 /= k;
        std::cout << (n - k + 2) / 2 * sum1 * k / (n - k + 1) << " "
                  << all - (n - k + 2) / 2 * sum1 * k / (n - k + 1) << "\n";
        return;
    }
    sum1 /= k;
    sum2 /= (n - k);
    std::cout << (n - k + 2) / 2 * sum1 * k / (n - k + 1) +
                     (n - k + 1) / 2 * sum2
              << " "
              << all - (n - k + 2) / 2 * sum1 * k / (n - k + 1) -
                     (n - k + 1) / 2 * sum2
              << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

G

题意

交互题。

给定一棵树的大小 \(n\)，\(\lceil\frac{n}{2}\rceil\) 次询问，每次询问一个节点，回答所有节点到该节点到距离，求这棵树。

题解

询问次数容易想到按照深度分组，我们先询问一次，得出各节点的深度奇偶。那么一定有一组的大小是 \(\lfloor\frac{n-1}{2}\rfloor = \lceil\frac{n}{2}\rceil - 1\)，我们询问所有节点即可构造出这棵树，恰好 \(\lceil\frac{n}{2}\rceil\)​ 次询问。

时间复杂度：\(O(n^2s)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    std::cin >> n;
    std::vector<int> d(n + 1), d0, d1;
    auto query = [&](int x) {
        std::cout << "? " << x << std::endl;
        for (int i = 1; i <= n; i++) {
            std::cin >> d[i];
        }
    };
    query(1);
    std::vector<std::vector<int>> adj(n + 1);
    for (int i = 2; i <= n; i++) {
        if (d[i] == 1) {
            adj[1].push_back(i);
        }
        if (d[i] & 1) {
            d1.push_back(i);
        } else {
            d0.push_back(i);
        }
    }
    if (d0.size() > d1.size()) {
        std::swap(d0, d1);
    }
    for (auto x : d0) {
        query(x);
        for (int i = 2; i <= n; i++) {
            if (d[i] == 1) {
                adj[x].push_back(i);
            }
        }
    }
    std::cout << "!" << std::endl;
    for (int i = 1; i <= n; i++) {
        for (auto y : adj[i]) {
            std::cout << i << " " << y << std::endl;
        }
    }

    return 0;
}

J

题意

给定 \(n\) 个数和一个数 \(k\)，可以选择一个区间 \([l,r]\)，将 \(a_l,a_{l+1},...,a_r\) 都加 \(k\)，求能获得的最大所有数的 gcd。

题解

gcd 的题一般都是枚举，具有性质：\((a,b) = (b, \mid a- b\mid)，(a,b,c) = (\mid a-b\mid,\mid c-b\mid, c)\)。

假设我们选择区间 \([l,r]\)，那么整个序列的 gcd 可以表示为：

\(((a_1,...,a_{l-1}),(\mid a_{l+1}-a_{l}\mid,\mid a_{l+2}-a_l\mid,...,\mid a_{r} - ar_{r-1}\mid),a_{r}+k,(a_{r+1},...,a_n))\)​。

这样，我们通过 gcd 的性质转化为单点加 \(k\)。

我们想让 gcd 最大，重点是第二项，假设对于 \(l-1\in[L,R]\) 前缀 gcd 都相同，此时我们让第二项的长度尽可能小才最优，即令 \(l = R-1\)，接着我们就可以枚举后面的位置单点加 \(k\) 求 gcd 最大值。

由于前缀 gcd 每减少一次，至少减少 2，因此枚举这样的区间 \([L,R]\) 的次数是 \(O(\log)\) 的。还要特别注意前缀 gcd 全部相同的情况。

时间复杂度：\(O(n\log n)\)​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using u128 = unsigned __int128;

void solve() {
    int n;
    i64 k;
    std::cin >> n >> k;
    std::vector<i64> a(n + 1), pre(n + 1), suf(n + 2);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
        pre[i] = std::gcd(pre[i - 1], a[i]);
    }
    for (int i = n; i >= 1; i--) {
        suf[i] = std::gcd(suf[i + 1], a[i]);
    }
    i64 ans = pre[n];

    for (int i = 1, l; i <= n; i = l + 1) {
        l = i;
        while (l <= n && pre[l] == pre[l - 1]) {
            l++;
        }

        i64 res = pre[l - 1];
        for (int r = l; r <= n; r++) {
            if (r > l) {
                res = std::gcd(res, std::abs(a[r] - a[r - 1]));
            }
            ans = std::max(ans, std::gcd(res, std::gcd(a[r] + k, suf[r + 1])));
        }
    }

    std::cout << ans << "\n";
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int T;
    std::cin >> T;
    while (T--) {
        solve();
    }

    return 0;
}