ACM八月训练 & UESTC 暑假二轮集训

发表于 2025-07-30 更新于 2025-09-01 分类于 ACM 阅读次数：本文字数： 89k

终于进队啦，不容易啊！接下来是组队训练！

7 月 30 日 Round 1

第一次组队训练垫底了qwq 补题发现怎么全是 easy 呀，交互没想到太可惜了...

D

题意

$n$ 种组织，每个组织有 $a_i$ 个人，求方案数：选择一些组织，它们的人数和严格大于总人数的一半，并且去掉任意一个组织的人，它们的人数和小于等于总人数的一半。

题解

设 $half = \frac{\sum a_i}{2}$，那么要求可以转化为 $\sum_{i\in S}a_i > half,\sum_{i\in S}a_i - \min_{i\in S} a_i \le half$。

我们不妨枚举每一个数作为最小值，那么就是比它大的数可以作为一个 01 背包来算方案数，从大到小排序后朴素枚举每一个数之前位置的背包是 $O(n^2q)$ 的，实际上可以在 0-1 背包的过程中计算，复杂度 $O(nq)$

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    std::cin >> n;
    std::vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
    }
    sort(a.begin() + 1, a.end(), std::greater());
    i64 ans = 0;
    int sum = accumulate(a.begin() + 1, a.end(), 0);
    int half = sum / 2;
    std::vector<i64> dp(sum + 1);
    dp[0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = sum; j >= a[i]; j--) {
            if (j + a[i] > half && j <= half) {
                ans += dp[j];
            }
            dp[j] += dp[j - a[i]];
        }
    }
    std::cout << ans << "\n";

    return 0;
}

H

题意

交互题。有一个函数 $f(x)$，值域为 $[1,n]$，可以询问 $f^c(r),r,c\in[1,n]$ 1000 次，求出一个位置 $x$ 满足 $f^c(x) = c$。

题解

诈骗题啊。问 $f^n(1) = t$ 和 $f^{n-t}(1) = s$，那么一定有 $f^{t}(s) =t$，注意特判 $s = n$。两次就行。

1000 次的解法是询问 $\{1,2,...,\sqrt{n},2\sqrt{n},3\sqrt{n},...,\sqrt{n}\times \sqrt{n}\}$，不过我赛时和下来一直 WA，先放着吧。

#include <bits/stdc++.h>

using i64 = long long;
#define int long long
signed main(void) {
    std::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);

    int n;
    std::cin >> n;
    auto query = [&](int c, int r) {
        std::cout << "? " << c << " " << r << std::endl;
        int x;
        std::cin >> x;
        return x;
    };
    auto answer = [&](int c, int r) {
        std::cout << "! " << c << " " << r << std::endl;
    };
    if (n == 1) {
        answer(1, 1);
        return 0;
    }
    int t = query(n, 1);
    if (n == t) {
        answer(n, 1);
        return 0;
    }
    int s = query(n - t, 1);
    answer(t, s);

    return 0;
}

K

题意

给定一张无向图，有边权，在 $k$ 个点放置饼干店，走到该处能买到饼干的概率是 $p_i$，从 $1$ 走到 $n$ ，求出能买到饼干的最短路的期望，如果可能买不到输出“impossible”。

题解

impossible 就是看有没有 $p_i = 1$，没有的话就不可能。

要最短路，我们的想法是先贪心地看最短路上能不能买到，不能的话继续看次短路，贡献是前面不能买到的概率乘该条路上能买到的概率，再乘最短路长度。那么我们关心的就是怎么找次短路。

我们可以钦定在每个饼干店 $i $ 购买，那么对应的路径长度就是从 1 到 $i$ 的最短路，加上从 $i$ 到 $n$ 的最短路。那么我们从 1 跑一次 Dijkstra，从 $n$ 跑一次 Dijkstra，根据两次的距离相加排序即可。而根据抽签公平性，同一条最短路上的点，选择的顺序可以是任意的。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m, k;
    std::cin >> n >> m >> k;
    std::vector<std::vector<std::array<int, 2>>> adj(n + 1);
    for (int i = 1; i <= m; i++) {
        int x, y, l;
        std::cin >> x >> y >> l;
        adj[x].push_back({y, l});
        adj[y].push_back({x, l});
    }
    bool ok = false;
    std::vector<std::pair<int, double>> p;
    for (int i = 1; i <= k; i++) {
        int x;
        double pr;
        std::cin >> x >> pr;
        p.push_back({x, pr});
        if (pr == 1.0) {
            ok = true;
        }
    }
    if (!ok) {
        std::cout << "impossible\n";
        return 0;
    }
    std::vector<i64> dis1(n + 1, 1e18), dis2(n + 1, 1e18);
    auto dijkstra = [&](int s = 1, std::vector<i64> & dis) {
        std::vector<bool> vis(n + 1);
        using PII = std::pair<i64, int>;
        std::priority_queue<PII, std::vector<PII>, std::greater<>> pq;
        pq.push({0, s});
        dis[s] = 0;
        while (!pq.empty()) {
            auto [_, x] = pq.top();
            pq.pop();
            if (vis[x]) {
                continue;
            }
            vis[x] = true;
            for (auto [y, w] : adj[x]) {
                if (dis[y] > dis[x] + w) {
                    dis[y] = dis[x] + w;
                    pq.push({dis[y], y});
                }
            }
        }
    };
    dijkstra(1, dis1);
    dijkstra(n, dis2);
    sort(p.begin(), p.end(), [&](auto i, auto j) {
        return dis1[i.first] + dis2[i.first] < dis1[j.first] + dis2[j.first];
    });
    double pre = 1.0;
    double ans = 0;
    for (auto [x, pr] : p) {
        ans += (dis1[x] + dis2[x]) * pre * pr;
        pre *= (1 - pr);
    }
    std::cout << std::fixed << std::setprecision(10) << ans << "\n";

    return 0;
}

L

题意

一个书架有 $n$ 层，每个书架能放 $x$ 本书，每一层的高度是 $a_i$，有 $m$ 本书，每本书高度 $b_i$，现在想在一些书架放装饰品，每层书架最多放一个，如果放装饰品，该层书架只能装 $y$ 本书，求能放的最多装饰品个数。

题解

求最大值可以二分，考虑如何 check。

我们肯定是贪心地把装饰品往高度较低的书架放的，否则可能会有一些书不能放置在高度更低的地方。那么排序后模拟放置即可。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m, x, y;
    std::cin >> n >> m >> x >> y;
    std::vector<int> a(n + 1), b(m + 1);
    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
    }
    for (int i = 1; i <= m; i++) {
        std::cin >> b[i];
    }
    sort(a.begin() + 1, a.end());
    sort(b.begin() + 1, b.end());
    int lo = 0, hi = n;
    int ans = -1;
    while (lo <= hi) {
        int mid = lo + (hi - lo) / 2;
        auto check = [&](int mid) {
            std::vector<int> l(n + 1, x);
            for (int i = 1; i <= mid; i++) {
                l[i] = y;
            }
            for (int i = 1, j = 1; i <= m; i++) {
                if (l[j] >= 1 && b[i] <= a[j]) {
                    l[j]--;
                } else {
                    while (l[j] == 0 || b[i] > a[j]) {
                        j++;
                        if (j > n) {
                            return false;
                        }
                    }
                    l[j]--;
                }
            }
            return true;
        };
        if (check(mid)) {
            lo = mid + 1;
            ans = std::max(ans, mid);
        } else {
            hi = mid - 1;
        }
    }
    if (ans == -1) {
        std::cout << "impossible\n";
        return 0;
    }
    std::cout << ans << "\n";

    return 0;
}

M

题意

给定一个凸多边形，求所有顶点在凸多边形顶点上的三角形面积之后与凸多边形面积的比值。

题解

纠正一个自己的误区，叉乘求面积，$ $ 要求 $ $ 在 $ $ 的逆时针方向上，而不是要求这两个向量的起点相同。

因此，由于凸多边形的点是逆时针方向给的，三角形面积之和为（以下 1-index，代码是 0-index）： $$ \[\begin{align*} &\sum_{i<j<k}(p_j-p_i)\times(p_k-p_j)\\\\ &=\sum_j((j-1)p_j - \sum_{i<j}p_i)\times(\sum_{k>j}p_k-(n-j)p_j)\\\\ \end{align*}\] $$ 求凸多边形面积，从原点取相邻顶点的向量叉乘即可，记得都要除以 2。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using std::abs, std::max, std::min, std::swap;
using std::numeric_limits;
using std::pair, std::make_pair;
using std::set, std::multiset;
using std::tuple, std::make_tuple;
using std::vector, std::deque;

using T = long double;  // 全局数据类型

constexpr T eps = 1e-8;
constexpr T INF = numeric_limits<T>::max();
constexpr T PI = 3.1415926535897932384l;

// 点与向量
struct Point {
    T x, y;

    bool operator==(const Point &a) const {
        return (abs(x - a.x) <= eps && abs(y - a.y) <= eps);
    }
    bool operator<(const Point &a) const {
        if (abs(x - a.x) <= eps) return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const Point &a) const { return !(*this < a || *this == a); }
    Point operator+(const Point &a) const { return {x + a.x, y + a.y}; }
    Point operator-(const Point &a) const { return {x - a.x, y - a.y}; }
    Point operator-() const { return {-x, -y}; }
    Point operator*(const T k) const { return {k * x, k * y}; }
    Point operator/(const T k) const { return {x / k, y / k}; }
    T operator*(const Point &a) const { return x * a.x + y * a.y; }  // 点积
    T operator^(const Point &a) const {
        return x * a.y - y * a.x;
    }  // 叉积，注意优先级
    int toleft(const Point &a) const {
        const auto t = (*this) ^ a;
        return (t > eps) - (t < -eps);
    }  // to-left 测试
    T len2() const { return (*this) * (*this); }  // 向量长度的平方
    T dis2(const Point &a) const {
        return (a - (*this)).len2();
    }  // 两点距离的平方
    int quad() const  // 象限判断 0:原点 1:x轴正 2:第一象限 3:y轴正 4:第二象限
                      // 5:x轴负 6:第三象限 7:y轴负 8:第四象限
    {
        if (abs(x) <= eps && abs(y) <= eps) return 0;
        if (abs(y) <= eps) return x > eps ? 1 : 5;
        if (abs(x) <= eps) return y > eps ? 3 : 7;
        return y > eps ? (x > eps ? 2 : 4) : (x > eps ? 8 : 6);
    }

    // 必须用浮点数
    T len() const { return sqrtl(len2()); }                 // 向量长度
    T dis(const Point &a) const { return sqrtl(dis2(a)); }  // 两点距离
    T ang(const Point &a) const {
        return acosl(max(-1.0l, min(1.0l, ((*this) * a) / (len() * a.len()))));
    }  // 向量夹角
    Point rot(const T rad) const {
        return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
    }  // 逆时针旋转（给定角度）
    Point rot(const T cosr, const T sinr) const {
        return {x * cosr - y * sinr, x * sinr + y * cosr};
    }  // 逆时针旋转（给定角度的正弦与余弦）
};

// 极角排序
struct Argcmp {
    bool operator()(const Point &a, const Point &b) const {
        const int qa = a.quad(), qb = b.quad();
        if (qa != qb) return qa < qb;
        const auto t = a ^ b;
        // if (abs(t)<=eps) return a*a<b*b-eps;  // 不同长度的向量需要分开
        return t > eps;
    }
};
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    std::cin >> n;
    vector<Point> p(n);
    std::vector<T> prex(n + 1), prey(n + 1), sufx(n + 2), sufy(n + 2);
    for (int i = 0; i < n; i++) {
        int x, y;
        std::cin >> x >> y;
        p[i] = {(T)x, (T)y};
    }
    for (int i = 1; i <= n; i++) {
        prex[i] = prex[i - 1] + p[i - 1].x;
        prey[i] = prey[i - 1] + p[i - 1].y;
    }
    for (int i = n; i >= 1; i--) {
        sufx[i] = sufx[i + 1] + p[i - 1].x;
        sufy[i] = sufy[i + 1] + p[i - 1].y;
    }
    auto nxt = [&](int i) { return i + 1 == n ? 0 : i + 1; };
    auto get_area = [&]() {
        T ans = 0;
        for (int i = 0; i < n; i++) {
            ans += p[i] ^ p[nxt(i)];
        }
        return abs(ans) / 2;
    };
    T area = get_area();
    T sum = 0;
    for (int j = 0; j < n; j++) {
        sum += (Point(j * p[j].x - prex[j], j * p[j].y - prey[j]) ^
                Point(sufx[j + 2] - (n - j - 1) * p[j].x,
                      sufy[j + 2] - (n - j - 1) * p[j].y)) /
               2;
    }
    std::cout << std::fixed<<std::setprecision(10) << sum / area << "\n";

	return 0;
}

7 月 31 日 Round 2

加训加训！

J

题意

给定世界地图上一些坐标，依次走过这些坐标，由于有两个方向走，优先走距离更短的，且最后走回出发点，求是否能走遍所有经度，如果不能，输出一个经度（以 .0 或 .5）结尾。

题解

这种输出格式，一般将坐标乘二后处理更方便，将负数全部变成正数也更方便。对于要去的目的地，可以判断距离是否大于一半，如果大于一半就要走相反方向，通过地图的边缘到达，否则直接朝着目标走就行了。通过差分数组维护行走的区间，最后看是否有区间未走即可。

#include <bits/stdc++.h>

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    std::vector<int> a(722);
    int n;
    std::cin >> n;
    int last;
    std::cin >> last >> last;
    last += 180;
    last *= 2;
    int start = last;
    bool ok = false;
    for (int i = 2; i <= n; i++) {
        int x, y;
        std::cin >> x >> y;
        y += 180;
        y *= 2;
        if (abs(y - last) == 360) {
            ok = true;
            continue;
        } else {
            int st = std::min(last, y), ed = std::max(last, y);
            if (ed - st < 360) {
                a[st]++, a[ed + 1]--;
            } else {
                a[0]++, a[st + 1]--, a[ed]++;
            }
        }
        last = y;
    }
    if (ok) {
        std::cout << "yes\n";
        return 0;
    }
    int st = std::min(last, start), ed = std::max(last, start);

    if (ed - st < 360) {
        a[st]++, a[ed + 1]--;
    } else {
        a[0]++, a[st + 1]--, a[ed]++;
    }
    for (int i = 1; i <= 720; i++) {
        a[i] += a[i - 1];
    }
    std::cout << "\n";
    for (int i = 0; i <= 720; i++) {
        if (a[i] == 0) {
            std::cout << "no ";
            std::cout << std::fixed << std::setprecision(1) << i / 2.0 - 180
                      << "\n";
            return 0;
        }
    }
    std::cout << "yes\n";

    return 0;
}

8 月 1 日 Round 3

封榜后过三题 + 最后一分钟过题，刺激！

C

题意

交互题。有一张图，节点数 $n\le 200$，3500 次询问判断它是否是连通的，每次可以询问一个子集，回答有多少子集以外的节点和子集里至少一个点相连。

题解

3500 / 200 < 18，想到二分啊！！！

我们考虑询问集合 $A,B,C = A\cup B$，且 $A,B$ 完全不相交，答案分别记作 $f(A),f(B),f(C)$，那么如果 $f(A) + f(B)\ne f(C)$，说明要么 $A$ 集合的点与 $B$ 集合的点有连边，要么 $A,B$ 集合同时连向了一个不属于它们的点。

考虑如何判断答案，我们可以从 1 开始询问，直到将 1 可达的所有节点都放在同一个集合中，问题转换为如何寻找到 1 可达的节点。考虑维护一个集合 $A$，初始只有 1 节点，每次二分出一个最小的节点满足从 $A$ 现有的节点可以到达它。具体过程为，设该节点为 $x$，我们询问 $f(A)$，维护一个 $B$ 集合表示不在 $A$ 中的节点，在 $B$ 集合二分，询问 $B$ 集合左边的子集，如果满足 $f(A) + f(B)\ne f(C)$，说明左侧至少有一个节点满足条件，继续二分缩小答案直到找到最小的节点，并从 $B$ 中删除，加入 $A$。如果询问中途我们遇到 $f(A) = 0$ 就可以判定图不连通了，否则我们一定可以找到这样的节点。

询问次数是 $O(2n\log n)$。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    string t(n, '0');
    vector<int> a(1), b(n - 1);
    iota(b.begin(), b.end(), 1);
    auto query1 = [&](vector<int> &a) {
        string s = t;
        for (auto i : a) {
            s[i] = '1';
        }
        cout << "? " << s << endl;
        int x;
        cin >> x;
        return x;
    };
    auto query2 = [&](vector<int> &a, vector<int> &b) {
        string s = t;
        for (auto i : a) {
            s[i] = '1';
        }
        for (auto i : b) {
            s[i] = '1';
        }
        cout << "? " << s << endl;
        int x;
        cin >> x;
        return x;
    };
    auto answer = [&](int x) { cout << "! " << x << endl; };
    while (a.size() < n) {
        auto x = query1(a);
        if (x == 0) {
            answer(0);
            return 0;
        }
        int lo = 0, hi = b.size() - 1;
        int ans = -1;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            vector tmp(b.begin() + lo, b.begin() + mid + 1);
            int y = query1(tmp);
            int z = query2(a, tmp);
            if (x + y != z) {
                ans = mid;
                hi = mid - 1;
            } else {
                lo = mid + 1;
            }
        }
        a.push_back(b[ans]);
        b.erase(b.begin() + ans);
    }
    answer(1);

    return 0;
}

D

题意

博弈。有 $n$ 堆糖果，Donkey 和 Puss in Boots 轮流行动，Donkey 先手。Donkey 只能选择一堆糖果拿至少 1 个，Puss in Boots 可以需要进行 $n$ 次操作，每次操作和 Donkey 相同。不能行动的失败，决定获胜者。

题解

Puss in Boots 进行 $n$ 次操作意味着他可以拿所有糖果，那么只要个数大于等于 $n$ 他就可以拿完，因此 Donkey 必须拿最大的使得剩下的糖果总和尽量小。注意特判全部为 0 的情况。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    if (count(a.begin() + 1, a.end(), 0) == n) {
        cout << "Puss in Boots\n";
        return 0;
    }
    if (accumulate(a.begin() + 1, a.end(), 0ll) -
            *max_element(a.begin() + 1, a.end()) <
        n) {
        cout << "Donkey\n";
    } else {
        cout << "Puss in Boots\n";
    }

    return 0;
}

G

题意

找出最长的子序列，满足每一个数都有一个相同的数与之相邻。

题解

简单 dp，设 $dp_i$ 表示前 $i$ 个位置的最长满足条件的子序列，设 $last[a[i]]$ 为上一次出现 $a[i]$ 的位置，那么有 $dp_{i} = (dp_{i-1}, dp_{last[ai]-1}+2,dp_{last[ai]} +1) $，第二项代表当前是第二个相同的数，第三项则代表三个及以上相同的数的答案。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int ans = 0;
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    map<int, int> mp;
    vector<int> dp(n + 1);
    for (int i = 1; i <= n; i++) {
        dp[i] = dp[i - 1];
        if (mp.count(a[i])) {
            dp[i] = max({dp[i - 1], dp[mp[a[i]] - 1] + 2, dp[mp[a[i]]] + 1});
        }
        ans = max(ans, dp[i]);
        mp[a[i]] = i;
    }
    cout << ans << "\n";

    return 0;
}

J

题意

$n$ 个生物的栖息地环形排列，每个生物喜欢的温度是 $t_i$，每天可以选择连续的三个生物，将其中一个生物喜欢的温度改成三者最大值或最小值。求对于每个 $t_i$ 各需要多少天让所有生物喜欢的温度都变成 $t_i$。

题解

如果 $t_i$ 可以作为某个三元组的最值，那么答案就是 $n - cnt_{t_i}$，否则需要额外的一次操作，将某个三元组的另一个数变为最值，然后 $t_i$ 就能作为最值了，答案是 $n -cnt_{t_i} + 1$。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    vector<bool> mx(1e5 + 1), mn(1e5 + 1);
    int n;
    cin >> n;
    vector<int> a(n + 1), cnt(1e5 + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        cnt[a[i]]++;
    }
    for (int i = 1; i <= n; i++) {
        auto l = [&](int x) { return x - 1 == 0 ? n : x - 1; };
        auto r = [&](int x) { return x + 1 > n ? 1 : x + 1; };
        if (max({a[l(i)], a[l(l(i))], a[i]}) == a[i]) {
            mx[a[i]] = true;
        }
        if (min({a[l(i)], a[l(l(i))], a[i]}) == a[i]) {
            mn[a[i]] = true;
        }
        if (max({a[r(i)], a[r(r(i))], a[i]}) == a[i]) {
            mx[a[i]] = true;
        }
        if (min({a[r(i)], a[r(r(i))], a[i]}) == a[i]) {
            mn[a[i]] = true;
        }
        if (max({a[r(i)], a[l(i)], a[i]}) == a[i]) {
            mx[a[i]] = true;
        }
        if (min({a[r(i)], a[l(i)], a[i]}) == a[i]) {
            mn[a[i]] = true;
        }
    }
    for (int i = 1; i <= n; i++) {
        if (mx[a[i]] || mn[a[i]]) {
            cout << n - cnt[a[i]] << " \n"[i == n];
        } else {
            cout << n - cnt[a[i]] + 1 << " \n"[i == n];
        }
    }

    return 0;
}

L

题意

给定一个排列，通过一些操作将其恢复成正序。可以选择一个位置 $i$，将 $i$ 位置移到 $j$ 位置，同时 $j$ 位置开始的元素都往后移一位，代价为 $j$，求最小代价以及具体方案。

题解

答案有一个上界是 $n$，方法是依次将 $n$ 到 1 都移到 1 位置，考虑如何减少移动次数。

一个观察是，我们不需要把 $i$ 移到 $j > i$ 的位置 $j$，因为这样做等价于先把满足 $i < p\le j$ 的位置都按顺序移到 1，再把原来 $p < i$ 的位置都移到 1，可以达到同样的效果，但只需要 $j - 1$ 的代价。（观察一）

其次，我们要把 $i$ 移到 $j < i$ 的位置 $j$，等价于先把 $i$ 移到 1，再把原来满足 $p < i$ 的位置依次移到 1，也能达成同样的效果，代价是 $j$，因此我们可以把操作都看成移到 1 位置。（观察二）

有了上面的结论，我们考虑优化答案的上界，我们记录下所有不在正确顺序的位置，先处理对应 $p$ 值较大的（把它先移到 1），再处理值较小的，这样的答案是最优的。

考虑输出答案，前面每移动一个 1，理论上后面的位置会往后挪一个，但是如果后面的位置在前面处理的位置的后面就不受影响了，因此可以通过一个树状数组记录偏移量。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

struct Fenwick {
    int n;
    std::vector<i64> a;
    Fenwick(int n = 0) { init(n); }
    void init(int n_) {
        n = n_;
        a.assign(n_ + 1, 0);
    }
    void add(int x, i64 v) {
        for (int i = x; i <= n; i += i & -i) {
            a[i] += v;
        }
    }
    i64 sum(int x) {
        i64 res = 0;
        for (int i = x; i >= 1; i -= i & -i) {
            res += a[i];
        }
        return res;
    }
    i64 rangeSum(int l, int r) { return sum(r) - sum(l - 1); }
};

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    vector<int> v;
    for (int i = n, t = n; i >= 1; i--) {
        if (a[i] == t) {
            t--;
        } else {
            v.push_back(i);
        }
    }
    sort(v.begin(), v.end(), [&](auto i, auto j) { return a[i] > a[j]; });
    Fenwick bit(n);
    cout << v.size() << " " << v.size() << "\n";
    for (int i = 0; i < v.size(); i++) {
        cout << v[i] + i - bit.sum(v[i]) << " " << 1 << "\n";
        bit.add(v[i], 1);
    }

    return 0;
}

8 月 2 日 Round 4

G

题意

给定 $n$，求节点数为 $n$ 的有标号树中，有多少棵树存在完美匹配。

题解

显然 $n$ 必须是偶数。并且一棵树如果存在完美匹配，这些匹配的形态是唯一的，即固定两个位置配对。那么我们不妨把完美匹配的两点缩成一个点，这样的方案数是 $(n-1)!!$，因为对于第一个点，可以与 $n-1$ 个点配对，然后还剩下 $n-2$ 个点，递归处理。然后我们可以用这些点来构造一棵有标号树。根据 Cayley 公式， $K_n$ 有 $n^{n-2}$ 棵生成树，同时，还需要考虑连边的两点 $(a,b),(c,d)$ 的连接方式，一共有四种，且有 $\frac{n}{2} - 1$ 条边。因此答案就是 $(n-1)!!\times \frac{n}{2}^{\frac{n}{2}-2}\times 4^{\frac{n}{2} - 1}$。

8 月 4 日 Round 5

先补一下 3 号的 ARC 和 2 号的 ABC 的题。

ARC 203 C

题意

一个 $H\times W$ 的方格图，每相邻两个格子之间有一条边，求选择 $k$ 条边的方案数，满足能从左上角的格子走到右下角。

$T,H,W\le 2\times 10^5,K\le H + W$

题解

注意数据范围，多测没有变量总和的限制，也没有 $H\times W$ 的限制，一定是推公式。

显然有方案需要 $k\ge H + W - 2$，而 $k\le H +W$，不妨分成三类讨论。

当 $k = H + W - 2$ 时，就是一条从左上角到右下角的路径，只能向下或向右，方案数为 $\begin{pmatrix}H + W - 2\\H - 1\end{pmatrix}$，含义为长度为 $H +W - 2$ 的序列，每个值都是向右或向下，从中选择 $H - 1$ 个向下。

当 $k = H + W - 1$ 时，就是在上面的基础上多一条边，随便选就行，可以选择的边的数量为 $H(W - 1) + W(H - 1) - (H + W - 2) = 2HW - 2H - 2W + 2 $，答案就是 $\begin{pmatrix}H + W - 2\\H - 1\end{pmatrix}\times(2HW - 2H - 2W + 2)$。

当 $k = H + W$ 时，除了只能向右或向下走一条路径，还可以在一个位置向左或向右，走一条距离刚好为 $H + W$ 的路径。如果最短路为 $H + W - 2$，不能简单地对于 $\begin{pmatrix}H + W - 2\\H - 1\end{pmatrix}$ 乘一个 $\begin{pmatrix}2HW - 2H - 2W + 2\\H - 1\end{pmatrix}$，因为加两条边可能会出现重复情况，且这种情况当且仅当 $(i,j)\rightarrow (i,j+1)\rightarrow(i+1,j+1)$ 和 $(i,j)\rightarrow(i+1,j)\rightarrow(i+1,j+1)$ 同时被选择，我们可以将这四块正方形看作一个整体，那么多出来的数量就变成了在 $(H - 1)\times (W - 1)$ 的方格图中走一条长度为 $H + W - 4$ 的正方形，因此多出来的数量就是 $\begin{pmatrix}H + W - 4\\H - 2\end{pmatrix}\times (H + W - 3)$，因为这 $H + W - 3$ 个正方形中任选一个，都可以拓展为四个小正方形，它们被重复计数了一次。

再考虑可以走一条距离刚好为 $H + W$ 的路径，不妨先考虑可以往左走一次，向上是同理的。如图，当我们在某个位置选择向左走时，它的前一步必须是向下，后一步必须是向下，否则均不符合题意。那么，我们可以选择一个向下的位置，钦定它的下一步往左走，还需要考虑到不能走出界，那么方案数为 $\begin{pmatrix}H + W - 2\\H - 3\end{pmatrix}\times(W - 1)$。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 998244353;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

struct Comb {
    int n;
    std::vector<Z> _fac;
    std::vector<Z> _invfac;
    std::vector<Z> _inv;

    Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
    Comb(int n) : Comb() { init(n); }

    void init(int m) {
        if (m <= n) return;
        _fac.resize(m + 1);
        _invfac.resize(m + 1);
        _inv.resize(m + 1);

        for (int i = n + 1; i <= m; i++) {
            _fac[i] = _fac[i - 1] * i;
        }
        _invfac[m] = _fac[m].inv();
        for (int i = m; i > n; i--) {
            _invfac[i - 1] = _invfac[i] * i;
            _inv[i] = _invfac[i] * _fac[i - 1];
        }
        n = m;
    }

    Z fac(int m) {
        if (m > n) init(2 * m);
        return _fac[m];
    }
    Z invfac(int m) {
        if (m > n) init(2 * m);
        return _invfac[m];
    }
    Z inv(int m) {
        if (m > n) init(2 * m);
        return _inv[m];
    }
    Z binom(int n, int m) {
        if (n < m || m < 0) return 0;
        return fac(n) * invfac(m) * invfac(n - m);
    }
} comb(200000);  // Z 类型全局初始化，D 类型需要局部初始化

void solve() {
    int n, m, k;
    cin >> n >> m >> k;
    if (k < n + m - 2) {
        cout << 0 << "\n";
        return;
    }
    if (k == n + m - 2) {
        cout << comb.binom(n + m - 2, n - 1) << "\n";
        return;
    }
    if (k == n + m - 1) {
        Z r = 2 * n * m - 2 * n - 2 * m + 2;
        cout << comb.binom(n + m - 2, n - 1) * r << "\n";
        return;
    }
    Z r = 2 * n * m - 2 * n - 2 * m + 2;
    Z ans = comb.binom(n + m - 2, n - 1) * r * (r - 1) / 2;
    ans -= comb.binom(n + m - 4, n - 2) * (n + m - 3);
    if (n >= 3) {
        ans += (m - 1) * comb.binom(n + m - 2, n - 3);
    }
    if (m >= 3) {
        ans += (n - 1) * comb.binom(n + m - 2, m - 3);
    }
    cout << ans << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

ABC 417 D

题意

$Q$ 次询问，每次给定一个心情 $x_i$，依次收到 $n$ 个礼物，每个礼物有 $p_i$ 心情值，如果大于等于当前心情，当前心情加 $a_i$，否则当前心情减少 $b_i$（最低为 0），求最终心情。

$p_i,a_i,b_i\le 500,x_i\le10^9$

题解

一开始读错题了，以为当前心情 $\ge p_i$ 就加 $a_i$，预处理 500 以内的答案就行了，大于 $500$ 直接加上 $a$ 的总和。

按照正确题意稍微麻烦一点，显然心情非常大时减少 $b$ 的总和就行，还是可以考虑预处理一些初始心情非常小的答案。由于 $b,p\le 500$，我们可以选择预处理 $mp[i][v]$ 代表当前是第 $i$ 个礼物，心情为 $v\le 1000$ 的最终答案，可以从后往前转移。

考虑回答询问，$x\le 1000$ 时答案就是 $mp[1][x]$，否则我们在 $b$ 的前缀和数组 $pre$ 里二分找到一个位置 $id$ 使得 $x-pre_{id} \le 1000$，这样答案就是 $mp[id+1][x-pre_{id}]$，可以通过 std::lower_bound(x - 1000) 实现。如果不存在的话直接减去 $b$ 的总和。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<int> p(n + 1), a(n + 1), b(n + 1), pre(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> p[i] >> a[i] >> b[i];
        pre[i] = pre[i - 1] + b[i];
    }
    vector mp(n + 1, vector<int>(1001));
    for (int i = 0; i <= 1000; i++) {
        if (i <= p[n]) {
            mp[n][i] = i + a[n];
        } else {
            mp[n][i] = i - b[n];
            if (mp[n][i] < 0) {
                mp[n][i] = 0;
            }
        }
    }
    for (int i = n - 1; i >= 1; i--) {
        for (int j = 0; j <= 1000; j++) {
            if (j <= p[i] && j + p[i] <= 1000) {
                mp[i][j] = mp[i + 1][j + a[i]];
            } else if (j > p[i]) {
                mp[i][j] = mp[i + 1][max(0ll, j - b[i])];
            }
        }
    }
    int q;
    cin >> q;
    while (q--) {
        int x;
        cin >> x;
        if (x <= 1000) {
            cout << mp[1][x] << "\n";
            continue;
        }
        auto id =
            lower_bound(pre.begin() + 1, pre.end(), x - 1000) - pre.begin();
        if (id >= n) {
            cout << x - pre[n] << "\n";
            continue;
        }
        cout << mp[id + 1][max(0ll, x - pre[id])] << "\n";
    }

    return 0;
}

8 月 5 日 Round 6

不会计数勒个不会计数。现在正在对着构造和计数题单猛刷。预计每天补题后做 3 道左右的构造，剩下时间全力梭哈计数。

E

题意

求出有多少数组 $a$ 和 $b$ 满足对于任意 $i<j$，有 $\min(a_i,b_j) = \min(a_j,b_i),a_i,b_i\le m$。

$n,m\le 10^6$

题解

我们更关心的是最小值的位置，如果当 $a=b$ 时一定成立，有 $m^n$ 个。

否则，$a\ne b$，一定存在一个位置 $pos$，满足 $a_{pos}\ne b_{pos}$，我们设 $pos$ 是所有满足 $a_i\ne b_i$ 的位置中，$\min(a_i,b_i)$ 最小的，即 $\min(a_{pos},b_{pos}) = \min_{a_i\ne b_i}\min(a_i,b_i)$。最难满足的条件一定是其余的 $i$ 与 $pos$。由于 $a_{pos}\ne b_{pos}$，不妨设 $x = a_{pos} < b_{pos}$，将最终答案乘 2。

考虑 $(a_i,b_{pos}) $ 与 $\min(a_{pos},b_i)$。如果 $b_i < x$，那么必须有 $a_i = b_i$ ；否则当 $b_i \ge x$时，$a_i = x$。也就是说，对于任意 $a\ne b$，只要给定 $b$，我们总能找到满足条件的 $a$，且这样的 $a$ 是唯一的。那么我们只需要求出有多少 $b$。注意在给定 $x$ 的情况下，必须有一个位置 $i$ 满足 $a_i = x, b_i > x$，这是唯一的限制。考虑反面，假设所有位置都是 $b_i\le x$，有 $x^n$ 种，因此这样的 $b$ 有 $m^n - x^n$ 种。

因此，答案就是 $m^n-\sum_{x=1}^{n-1}(m^n - x^n)$，时间复杂度：$O(m\log n)$。

CF1646 C

题意

$t$ 组数据，每组数据给定 $n$，将 $n$ 分解为最少数，满足每个数最多出现一次，且每个数要么是 2 的幂，要么是某个数的阶乘，输出个数。

$t\le 100,n\le 10^{12}$

题解

当 $n$ 是奇数时，我们必定会选择一个 1，只需要考虑偶数的情况。只选择 2 的幂的话，其实就是 __builtin_popcountll(n)，阶乘对答案的优化就是可以代替多个幂。$10^{12}$ 的数据范围，阶乘不超过 15，且 $2^{15} = 32768$，我们是可以暴力枚举选哪些阶乘的。

时间复杂度：$O(T\times 2^{15})$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

void solve() {
    int n;
    cin >> n;
    int frac = 1;
    vector<int> t;
    for (int i = 2;; i++) {
        frac *= i;
        if (frac > n) {
            break;
        }
        t.push_back(frac);
    }
    int ans = 2e9;
    bool ok = false;
    if (n & 1) {
        n--;
        ok = true;
    }
    vector<int> b;
    auto dfs = [&](auto dfs, int id) -> void {
        if (id == t.size()) {
            int x = n;
            int cnt = 0;
            for (auto v : b) {
                if (x >= v) {
                    x -= v;
                }
                cnt++;
            }
            cnt += __builtin_popcountll(x);
            ans = min(ans, cnt);
            return;
        }
        b.push_back(t[id]);
        dfs(dfs, id + 1);
        b.pop_back();
        dfs(dfs, id + 1);
    };
    dfs(dfs, 0);
    cout << ans + ok << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

CF1542 B

题解

给定 $a,b,n$，一个集合最开始有 1，可以通过将集合中的元素 $\times a$ 或 $+b$ 生成新的元素，求 $n$ 是否在集合中。

$t\le 10^5,n,a,b\le 10^9$

题解

一个结论是，这样的操作得到的数都具有 $a^x + yb$ 的形式。

证明：若 $\times a$，上面的数会变成 $a^{x+1} + (ay) b$，符合形式。若 $+b$，会变成 $a^x + (y + 1) b$，符合形式。

因此，我们可以枚举 $a$ 的幂判断，需要特判 $n = 1$ 和 $a = 1$ 的情况。

时间复杂度：$O(T\log n)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

void solve() {
    int n, a, b;
    cin >> n >> a >> b;
    if (n == 1) {
        cout << "Yes\n";
        return;
    }
    if ((n - 1) % b == 0) {
        cout << "Yes\n";
        return;
    }
    if (a == 1) {
        cout << "No\n";
        return;
    }
    int x = 1;
    for (int i = 1;; i++) {
        x *= a;
        if (x > n) {
            break;
        }
        if ((n - x) % b == 0) {
            cout << "Yes\n";
            return;
        }
    }
    cout << "No\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

8 月 6 日 Round 7

顶级坐牢场，经典看到一堆 998244353 就不会做题了。

I

题意

给定一个随机生成的序列 $a$，满足 $a_i\le 10^{12}$，求 $\sum_{i=1}^n\sum_{j=1}^n(a_i\bmod {a_j})^2$。

题解

考虑对于每一个数 $a_j$，像数论分块一样把对于 $t= \lfloor\frac{a_i}{a_j}\rfloor$ 值相同的所有 $i$ 打包计算。那么首先排序，且排序后相同 $t$ 也在一段连续的区间上，设为 $[p,q]$

那么对于每一个 $j$，答案为 $\sum_{i=1}^n(a_i\bmod{a_j})^2 = \sum_{i=p}^qa_i^2 - 2a_jt(\sum_{i=p}^qa_i) + (a_jt)^2(\sum_{i=p}^qa_i^0)$。

我们通过二分找到每一块的右边界，预处理一阶和二阶前缀和，即可快速算出每一块的答案。

这样做的前提是分块的数量不会太多，在随机数据下，设 $A = 10^{12}$，最大的 $t $ 为 $\lfloor\frac{A}{a_j}\rfloor$，那么块数的期望即为 $E(\lfloor\frac{A}{a_j}\rfloor) = \frac{1}{A}\sum_{i=1}^A\frac{A}{i} = \sum_{i=1}^A\frac{1}{i} = O(\log A)$。

因此，时间复杂度为 $O(n\log n\log A)$。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 998244353;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1);
    vector<Z> pre(n + 1), pre2(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a.begin() + 1, a.end());
    for (int i = 1; i <= n; i++) {
        pre[i] = pre[i - 1] + a[i];
        pre2[i] = pre2[i - 1] + Z(a[i]) * Z(a[i]);
    }
    Z ans = 0;
    for (int i = 1; i <= n; i++) {
        for (int l = 1, r; l <= n; l = r + 1) {
            int lo = l, hi = n;
            while (lo <= hi) {
                int mid = lo + (hi - lo) / 2;
                if (a[mid] / a[i] == a[l] / a[i]) {
                    r = mid;
                    lo = mid + 1;
                } else {
                    hi = mid - 1;
                }
            }
            ans +=
                pre2[r] - pre2[l - 1] -
                2 * Z(a[i]) * (a[l] / a[i]) * (pre[r] - pre[l - 1]) +
                Z(a[i]) * (a[l] / a[i]) * Z(a[i]) * (a[l] / a[i]) * (r - l + 1);
        }
    }
    cout << ans << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

CF1614 C

题意

给定若干区间 $[l,r]$ ，以及 $a_l\mid ...\mid a_r$，构造一个数组满足给定条件，输出这个数组所有子序列的异或值的和。

题解

这种位运算的题能按位拆开就按位拆开考虑。重点在于怎么求所有子序列的异或值的和。

在考虑第 $i$ 位时，要想这一位对答案有贡献，不能全是 0，我们设一共有 $x$ 个 1，那么就有 $n - x$ 个 0，对答案的贡献就是选择奇数个 1 的方案数乘以任意选取 0 的方案数，即 $\sum_{i=1,3,5,...}^x\begin{pmatrix}x\\i\end{pmatrix}\times 2^{n-x} = 2^{x-1}\times2^{n - x} = 2^{n - 1}$。

那么，我们得出一个结论，只要二进制下某一位有 1，就对答案有 $2^{n-1}$ 的贡献，我们把给定区间的或拿去求或即可。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

constexpr int P = 1e9 + 7;
int qpow(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) {
            res = res * a % P;
        }
        a = a * a % P;
        b /= 2;
    }
    return res;
}

void solve() {
    int n, m;
    cin >> n >> m;
    int ans = 0;
    for (int i = 1; i <= m; i++) {
        int l, r, x;
        cin >> l >> r >> x;
        ans |= x;
    }
    cout << ans * qpow(2, n - 1) % P << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

CF1611 D

题意

给定一棵树，指定根节点和一个排列 $p$，构造树的边权，要求将根节点到各节点的距离排序后，距离从小到大对应的节点恰好是 $p$，且距离不能重复。

题解

主要在距离不能重复那里卡了一下，实际上我们指定第 $i$ 个节点到根的距离是 $i$ 就行了（根节点特判距离是 0 ）。

可以用一个 std::set 存储当前能用的节点，初始只加入根节点，每用掉一个节点后就将它的儿子加入 set，代表这些儿子也能使用。每次操作先查找 $p_i$，set 中不存在的话就特判 -1。然后赋值边权就行了，为 $i - ans[fa]$，因为整段距离是 $i$，只看一条边的话要减去它的父亲到根节点的距离。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

void solve() {
    int n;
    cin >> n;
    int root = 1;
    vector<vector<int>> adj(n + 1);
    vector<int> fa(n + 1);
    for (int i = 1; i <= n; i++) {
        int b;
        cin >> b;
        if (i == b) {
            root = i;
            continue;
        }
        adj[b].push_back(i);
        fa[i] = b;
    }
    vector<int> p(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> p[i];
    }
    vector<int> ans(n + 1);
    vector<int> dep(n + 1);
    int id = 1;
    int dis = 0;
    set<int> st;
    st.insert(root);

    while (id <= n) {
        auto it = st.find(p[id]);
        if (it == st.end()) {
            cout << -1 << "\n";
            return;
        }
        if (p[id] == root) {
            ans[p[id]] = 0;
        } else {
            ans[p[id]] = id - dep[fa[p[id]]];
            dep[p[id]] = id;
        }
        for (auto y : adj[p[id]]) {
            st.insert(y);
        }
        st.erase(it);
        id++;
    }
    for (int i = 1; i <= n; i++) {
        cout << ans[i] << " \n"[i == n];
    }
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

P6146 [USACO20FEB] Help Yourself G

题意

给定 $n$ 条线段 $[l,r]$（端点互不相同），求 $2^n$ 个子集中线段的复杂度是多少，复杂度定义为将能合并的线段都合并后线段的数量。

题解

首先将线段按照左端点排序。我们设 $f_i$ 表示前 $i$ 条线段的复杂度总和，那么答案就是 $f_n$。

考虑转移，对于每条线段都有取和不取两种情况，不取的话，答案就加上 $f_{i-1}$；否则，答案就是 $f_{i-1}$ 加上能让这条线段单独作为答案的情况。我们设前 $i - 1$ 条线段有 $x$ 条线段与 $f_{i - 1}$ 不相交，那么答案就加上 $2^x$。

因此，转移为 $f_{i } = 2f_{i -1} + 2^x$，为了求出 $x$，我们可以用前缀和的方法，将每条线段的右端点加入数组，$x$ 就是有多少比 $l$ 小的右端点。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

constexpr int P = 1e9 + 7;
int qpow(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) {
            res = res * a % P;
        }
        a = a * a % P;
        b /= 2;
    }
    return res;
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<array<int, 3>> e(n + 1);
    vector<int> b(2 * n + 1);
    for (int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        e[i] = {l, r, i};
        b[r]++;
    }
    for (int i = 1; i <= 2 * n; i++) {
        b[i] += b[i - 1];
    }
    sort(e.begin() + 1, e.end());
    vector<int> dp(n + 1);
    for (int i = 1; i <= n; i++) {
        dp[i] = (2 * dp[i - 1] % P + qpow(2, b[e[i][0] - 1])) % P;
    }
    cout << dp[n] << "\n";

    return 0;
}

P6075 [JSOI2015] 子集选取

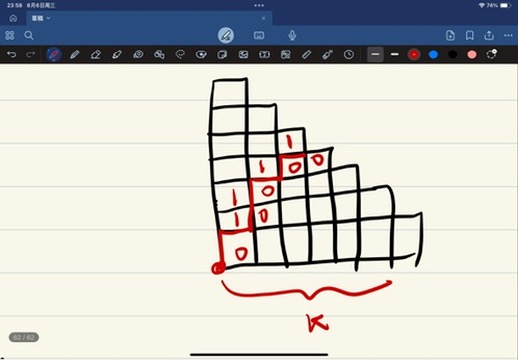
题意

$n$ 个元素的集合，选出若干子集组成一个边长为 $k$ 的三角形，要求 $A_{i-1,j}\subseteq A_{i,j},A_{i,j-1}\subseteq A_{i,j}$，求方案数。

题解

每个元素相互独立的，我们只需要求出一个元素的答案，将其 $n$ 次方即可得到最终的答案，关键在于如何求出一个元素的答案。

不妨考虑元素 1 和空集的情况。由于题目要求上面的集合应该包含下面和其右边的，整个三角形可以分成两片区域，左上方全是 1，右下方全是 0，这样的划分方式可以从最左下角的点开始划分分界线，在每个点都有 2 种路径：向上和向右可以走，一共走 $k$ 步，碰到边界就结束。因此答案就是 $2^k$，对于 $n$ 个元素相互独立，答案就是 $2^{nk}$。

CDBD4393-1C69-46D7-A978-6C35B50DD4E8_4_5005_c

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

constexpr int P = 1e9 + 7;
int qpow(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) {
            res = res * a % P;
        }
        a = a * a % P;
        b /= 2;
    }
    return res;
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, k;
    cin >> n >> k;
    cout << qpow(2, n * k) << "\n";

    return 0;
}

8 月 7 日 Round 8

前期队友嘎嘎过题，后面几道取模和几何就老实了。

B

题意

给定 $n$ 个点，判断是否存在三条直线，使得所有点都在直线上。

$n\le 10^4$

题解

直线数量很少，从这里出发，考虑怎么样才能找到这三条直线。

根据鸽笼原理，如果所有点都能被分成三条直线，我们要取 $k$ 条直线的话，任选 $k + 1$ 个点，两两组成的直线之间总有一条直线是在答案中的。那么我们从 $k = 3$ 递归下去处理 $k = 2,1$ 的情况，如果当前点集数量小于等于 $k$ 就一定能找到。对于每一个 $k$，就枚举 $\begin{pmatrix}k+1\\2\end{pmatrix}$ 条直线，对于每条直线，不在其上方的点就作为新的点集递归下去。注意判断三点总线的方法：两个向量求叉积。

时间复杂度：$O(\prod_{i=1}^3\begin{pmatrix}i+1\\2\end{pmatrix}\times n) = O(18n)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

using T = int;
constexpr T eps = 1e-8;
constexpr T INF = numeric_limits<T>::max();

// 点与向量
struct Point {
    T x, y;

    bool operator==(const Point &a) const {
        return (abs(x - a.x) <= eps && abs(y - a.y) <= eps);
    }
    bool operator<(const Point &a) const {
        if (abs(x - a.x) <= eps) return y < a.y - eps;
        return x < a.x - eps;
    }
    bool operator>(const Point &a) const { return !(*this < a || *this == a); }
    Point operator+(const Point &a) const { return {x + a.x, y + a.y}; }
    Point operator-(const Point &a) const { return {x - a.x, y - a.y}; }
    Point operator-() const { return {-x, -y}; }
    Point operator*(const T k) const { return {k * x, k * y}; }
    Point operator/(const T k) const { return {x / k, y / k}; }
    T operator*(const Point &a) const { return x * a.x + y * a.y; }  // 点积
    T operator^(const Point &a) const {
        return x * a.y - y * a.x;
    }  // 叉积，注意优先级
};

bool on_line(const Point &a, const Point &b, const Point &c) {
    return abs((a - b) ^ (a - c)) <= eps;
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<Point> p;
    for (int i = 1; i <= n; i++) {
        int x, y;
        cin >> x >> y;
        p.push_back({x, y});
    }
    auto dfs = [&](auto dfs, int k, vector<Point> &p) -> bool {
        if (p.size() <= k) {
            return true;
        }
        for (int i = 0; i <= k; i++) {
            for (int j = i + 1; j <= k; j++) {
                vector<Point> tmp;
                for (auto a : p) {
                    if (!on_line(a, p[i], p[j])) {
                        tmp.push_back(a);
                    }
                }
                if (dfs(dfs, k - 1, tmp)) {
    				return true;
    			}
            }
        }
        return false;
    };
    if (dfs(dfs, 3, p)) {
    	cout << "possible\n";
    } else {
    	cout << "impossible\n";
    }

    return 0;
}

F

题意

用 $1\times 2$ 的砖头砌一面 $n\times m$ 的墙，初始在一些位置底部放置一些 $1\times 1$ 的方格，判断能否刚好砌墙。

题解

考虑按列贪心，优先放置下面的，此时可能有一些位置无法放置，我们就在下一轮考虑它们。随着循环累积，这样无法放置的位置可能会非常多，一个一个考虑会超时，但是它们的相邻位置之差一定是 2，因此我们可以设置两个指针 $l,r$ 用来表示“凸起”的位置。

转移时讨论 $l,r$ 的关系，都不存在的话从下往上放 $1\times 2$ 即可，如果放不满就令 $l = r = m$。否则，我们考虑放置 $l$ 下方和 $r$ 上方会导致 $l, r$ 的变化即可。

时间复杂度：$O(n)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    cin >> n >> m;
    vector<int> h(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> h[i];
        if (h[i] > m) {
            cout << "impossible\n";
            return 0;
        }
    }
    int l = -1, r = -1;
    for (int i = 1; i < n; i++) {
        if (l == -1 && r == -1) {
            if ((m - h[i]) % 2 == 1) {
                l = r = m;
            }
            continue;
        }
        if (l <= h[i]) {
            cout << "impossible\n";
            return 0;
        }
        if ((l - h[i] + 1) % 2 == 1) {
            l--;
        } else {
            l++;
        }
        if ((m - r) % 2 == 1) {
            r++;
        } else {
            r--;
        }
        if (r < l) {
            l = r = -1;
        }
    }

    if (l == -1 && r == -1) {
        if ((m - h[n]) % 2 == 0) {
            cout << "possible\n";
        } else {
            cout << "impossible\n";
        }
        return 0;
    }
    if (l == r) {
        if ((m - r) % 2 == 0 && (l - h[n]) % 2 == 1) {
            cout << "possible\n";
        } else {
            cout << "impossible\n";
        }
        return 0;
    }
    cout << "impossible\n";

    return 0;
}

H

题意

假定每辆车都是 $1\times 2$ 大小的，构造一个 $n\times 2$ 的字符矩阵代表车位， $n \le 200$，$n$ 由自己选择。要求其中只含有 “#” 、“.” 两种字符，且 “#” 代表这里已经有车停了，“.” 代表这里为空。给定一个模意义下的方案数 $m$，构造一个矩阵，使得将车停满的方案数恰好为 $m$。

题解

计数 + 构造，太搞了。不妨先考虑连续的 $2\times i$ 的矩阵的方案数，那么考虑 dp，有 $f_i = f_{i-1} + f_{i-2}$，且 $f_1 = 1,f_2 = 2$，那么这道题就转化成了求若干斐波那契数的乘积在模意义下等于 $m$，并且总长度不超过 200（还需要考虑空隙）。

在模意义下除了搜索似乎很难解了，但是暴搜可以逼近 $2^{66}$，时间完全不足。不妨考虑一种类似 meet in the middle 的方案，在大小为 100 的矩阵里面搜索，使用哈希表存储搜索过的值，以及该步对应选择的斐波那契数的下标，搜索结束后对于每一个值查找它的逆元是否也在哈希表中，如果存在就可以构造答案。

复杂度和正确性主要取决于哈希表的大小，我们不能全部搜索，仍然会接近 $2^{33}$，但是我们可以定义一个最大哈希表的大小，一旦达到这个大小就停止，考虑当所有数都大致均匀分布的情况下，取 $limit = 10^6$ 可以得到 $10^{12}$ 种数，有很大概率覆盖 $10^9 + 7$。

此外，$n = 0$ 需要特判，构造一个不合法的方案即可。

时间复杂度：$O(limit)$。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

constexpr int P = 1e9 + 7;
int qpow(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) {
            res = res * a % P;
        }
        a = a * a % P;
        b /= 2;
    }
    return res;
}
int inv(int x) { return qpow(x, P - 2); }
constexpr int lim = 1e6;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    if (n == 0) {
        cout << "##.\n.##";
        return 0;
    }
    vector<int> fib(101), ifib(101);
    fib[1] = 1;
    fib[2] = 2;
    for (int i = 3; i <= 100; i++) {
        fib[i] = (fib[i - 1] + fib[i - 2]) % P;
    }
    for (int i = 1; i <= 100; i++) {
        ifib[i] = inv(fib[i]);
    }
    unordered_map<int, int> f, g;
    auto bfs = [&](int st, unordered_map<int, int> &f, vector<int> &fib) {
        queue<int> q;
        unordered_map<int, int> dis;
        q.push(st);
        f[st] = 0;
        dis[st] = 0;
        while (!q.empty() && f.size() < lim) {
            int now = q.front();
            q.pop();
            int step = dis[now];
            for (int i = 2; step + i + 1 <= 100; i++) {
                int to = now * fib[i] % P;
                if (f.count(to)) {
                    continue;
                }
                dis[to] = step + i + 1;
                f[to] = i;
                q.push(to);
            }
        }
    };
    bfs(1, f, fib);
    bfs(n, g, ifib);
    for (auto [val, step] : f) {
        if (g.count(val)) {
            string s = "";
            int cur = val;
            while (cur != 1) {
                int lst = f[cur];
                s += string(lst, '.') + "#";
                cur = cur * inv(fib[lst]) % P;
            }
            cur = val;
            while (cur != n) {
                int lst = g[cur];
                s += string(lst, '.') + "#";
                cur = cur * fib[lst] % P;
            }
            cout << s << "\n" << s << "\n";
            return 0;
        }
    }

    return 0;
}

8 月 8 日 Round 9

队友太强了 orz，精通随机化和乱搞过题。

A

题意

$n$ 种物品，每种物品有无限多个，第 $i$ 个物品的容量是 $i$，价值是 $a_i$，$q$ 次询问，每次给定一个背包的容量 $x$，求恰好装满背包的最小价值。且当背包容量 $ i n$ 时，必须拿第 $i$ 个物品。

$n\le 100, q\le 10^5,a_i,x\le 10^9$。

题解

变种背包问题，但是值域非常大。一个想法是，在容量很大时，我们可以贪心拿性价比最高的，在本题就是一直拿一种，使得价值加起来最小。我们可以设立一个极限值 $lim$ 远大于 $n$，当 $x \ge lim$ 时采取上述的贪心策略，否则使用背包问题解决。

尤其需要注意的是，背包问题求最小值需要先枚举容量！！！因为求最大值时，容量是从 0 开始的，如果选择第 $i$ 个是最优的方案，它会被累计起来直到达到容量，而求最大值的话，我们会先把 $dp$ 数组初始化无穷大，此时对于第 $i$ 种来说，转移到背包容量时的方案可能会被不优的覆盖掉（因为它从前面的容量转移过来，而前面的不一定是最优的），无法转移下去。而一旦错过第 $i$ 种，就再也不会拿这一种了。因此，我们需要在外层循环枚举容量，用类似递推的方法来转移。

还是不懂的话，放一个样例，可以自行打印一下 dp 数组，看看区别。

时间复杂度：$O(nq + n\times lim)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

constexpr int inf = 2e18;
constexpr int lim = 1e5;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, q;
    cin >> n >> q;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    vector<int> dp(lim + 1, inf);
    for (int i = 1; i <= n; i++) {
        dp[i] = a[i];
    }
    // for (int i = 1; i <= 10; i++) {
    //     cout << dp[i] << " \n"[i == 10];
    // }

    for (int j = n + 1; j <= lim; j++) {
        for (int i = 1; i <= n; i++) {
            dp[j] = min(dp[j], dp[j - i] + a[i]);
        }
        // for (int i = 1; i <= 10; i++) {
        //     cout << dp[i] << " \n"[i == 10];
        // }
    }

    while (q--) {
        int x;
        cin >> x;
        if (x <= lim) {
            cout << dp[x] << "\n";
            continue;
        }
        int ans = 2e18;
        for (int i = 1; i <= n; i++) {
            int cnt = (x - lim) / i;
            if ((x - lim) % i != 0) {
                cnt++;
            }
            ans = min(ans, cnt * a[i] + dp[x - i * cnt]);
        }
        cout << ans << "\n";
    }

    return 0;
}

I

题意

三个人，在一个有 $n$ 个岛屿的地方环形观光，观光结束后立刻离开。每个人在第个景点停留的时间为 $a_i,b_i,c_i$，从一个点到另一个点的时间三人相同为 $d_i$，问是否有方案选择三个人的起点，来使他们不会在某个岛相遇。

$n\le 400$

题解

最暴力的就是 $O(n^4)$ 枚举三个人的起点后判断是否可行，考虑优化。

如果 $a,b,c$ 互不冲突的话，可以转化为 $(a,b),(a,c),(b,c)$ 互不冲突，我们在上面的做法可以 $O(n^3)$ 枚举两个人的起点，求每两人之间的起点不会冲突的情况，然后再 $O(n^3)$ 枚举三个人的起点即可 $O(1)$ 判断。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

int st[3][3][410][410];

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<int> d(n);
    vector<vector<int>> a(3, vector<int>(n));
    for (int i = 0; i < n; i++) {
        cin >> d[i];
    }
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < n; j++) {
            cin >> a[i][j];
        }
    }
    for (int i = 0; i < 2; i++) {
        for (int j = i + 1; j < 3; j++) {
            for (int f = 0; f < n; f++) {
                vector<array<int, 2>> time(n);
                int now = 0;
                for (int s = f; s < f + n; s++) {
                    time[s % n] = {now, now + a[i][s % n]};
                    now += a[i][s % n] + d[s % n];
                }
                for (int s = 0; s < n; s++) {
                    now = 0;
                    bool ok = true;
                    for (int k = s; k < s + n; k++) {
                        int l = now, r = now + a[j][k % n];
                        if (l >= time[k % n][1] || r <= time[k % n][0]) {
                            now += a[j][k % n] + d[k % n];
                        } else {
                            ok = false;
                            break;
                        }
                    }
                    if (ok == true) {
                        st[i][j][f][s] = st[j][i][s][f] = 1;
                    }
                }
            }
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            for (int k = 0; k < n; k++) {
                if (st[0][1][i][j] == 1 && st[0][2][i][k] == 1 &&
                    st[1][2][j][k] == 1) {
                    cout << i + 1 << " " << j + 1 << " " << k + 1 << "\n";
                    return 0;
                }
            }
        }
    }
    cout << "impossible\n";

    return 0;
}

8 月 9 日 Round 10

最坐牢的一集，提前半小时润了（

E

题意

题解

8 月 11 日 Round 11

2025 北京邀请赛，4 题做大牢...

8 月 12 日 Round 12

2021 ICPC 沈阳，4 题铜牌区...

8 月 21 日及以后

回家后休息几天，慢慢开始补一下之前的题。

CF 2127 D

题意

给定一张简单连通图，求将相邻节点安排在河两边的方案数，只要有节点顺序不同即视为不同方案。

题解

初步想法是二分图的情况，仔细一想偶环也是不能有的，那么存在方案必须是树。

显而易见的是对于一个节点来说，它相邻的叶子节点是可以随意排列的，而相邻的非叶子节点必须放在两侧，所以如果非叶子节点超过 2 个，也是不存在方案的。我们考虑非叶子节点的贡献，就是对于相邻的叶子节点数量对应的阶乘，这样就不会重复。

同时注意将图镜像一下就会得到一种新的方案，将图中心对称也会得到一种新的方案，因此答案需要乘 4——只有一种情况例外，即只有一个非叶子节点时，因为此时两种情况等价。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

struct Comb {
    int n;
    std::vector<Z> _fac;
    std::vector<Z> _invfac;
    std::vector<Z> _inv;

    Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
    Comb(int n) : Comb() { init(n); }

    void init(int m) {
        if (m <= n) return;
        _fac.resize(m + 1);
        _invfac.resize(m + 1);
        _inv.resize(m + 1);

        for (int i = n + 1; i <= m; i++) {
            _fac[i] = _fac[i - 1] * i;
        }
        _invfac[m] = _fac[m].inv();
        for (int i = m; i > n; i--) {
            _invfac[i - 1] = _invfac[i] * i;
            _inv[i] = _invfac[i] * _fac[i - 1];
        }
        n = m;
    }

    Z fac(int m) {
        if (m > n) init(2 * m);
        return _fac[m];
    }
    Z invfac(int m) {
        if (m > n) init(2 * m);
        return _invfac[m];
    }
    Z inv(int m) {
        if (m > n) init(2 * m);
        return _inv[m];
    }
    Z binom(int n, int m) {
        if (n < m || m < 0) return 0;
        return fac(n) * invfac(m) * invfac(n - m);
    }
} comb(200000);  // Z 类型全局初始化，D 类型需要局部初始化

void solve() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> adj(n + 1);
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        adj[x].push_back(y);
        adj[y].push_back(x);
    }

    if (m != n - 1) {
        cout << 0 << "\n";
        return;
    }

    if (n == 2) {
        cout << 2 << "\n";
        return;
    }

    vector<int> deg(n + 1);
    Z ans = 4;
    for (int i = 1; i <= n; i++) {
        for (auto y : adj[i]) {
            if (adj[y].size() > 1) {
                deg[i]++;
            }
        }
        if (deg[i] > 2) {
            cout << 0 << "\n";
            return;
        }
        if (adj[i].size() > 1) {
            ans *= comb.fac(adj[i].size() - deg[i]);
            if (deg[i] == 0) {
                ans /= 2;
            }
        }
    }
    cout << ans << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

CF 2122 C

题意

给定 $n$ （偶数）个点，将它们两两配对，最大化每对点的曼哈顿距离之和。输出配对方案。

题解

对于一维的情况，选择当前集合中最小值和最大值配对即可。

现在扩展到二维，可以先排序固定一维，此时这一维的贡献确定了，且只要前一半和后一半配对就是最优的。接着考虑第二维，类似 CDQ 分治的做法，我们对对前一半和后一半分别排序，再首尾匹配，这样相当于找到一个四分点，对于两维都是最优的。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

void solve() {
    int n;
    cin >> n;
    vector<int> x(n + 1), y(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> x[i] >> y[i];
    }
    vector<int> order(n + 1);
    iota(order.begin(), order.end(), 0);
    sort(order.begin() + 1, order.end(),
         [&](auto &i, auto &j) { return x[i] < x[j]; });
    sort(order.begin() + 1, order.begin() + n / 2 + 1,
         [&](auto &i, auto &j) { return y[i] < y[j]; });
    sort(order.begin() + n / 2 + 1, order.end(),
         [&](auto &i, auto &j) { return y[i] < y[j]; });
    for (int i = 1; i <= n / 2; i++) {
        cout << order[i] << " " << order[n - i + 1] << "\n";
    }
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

CF 2132 D

题意

将 $[1,x]$ 的整数写在一起，即 1234567891011...，给定 $k$，求前 $k$ 位的数位和。

$t\le 2\times 10^4,k\le 10^{15}$

题解

不妨先找到前面完整的 $x$ 个数，再加上不完整的第 $x+1$ 个数。

一位数（1～9）有 9 个，两位数（10～99）有 90 个，三位数（100～999）有 900 个，我们可以求出位数相同的所有数的长度总和，通过二分即可求出 $x$ 的长度。我们将 $k$ 减去长度 $\le x$ 的长度的所有数的位数和，这样 $k$ 只表示相同长度的数字的位数和，通过整除长度即可求出 $x$，对长度取模即可知道 $x + 1$ 的位数。$x + 1$ 直接加上，$[1, x]$ 的和通过数位 dp 解决。

数位 dp 的 dfs 函数设状态为 pos（正在处理第几位），limit（该位是否存在限制），sta（考虑前导 0 的影响）。

如果该位为前导 0，直接递归到下一位，否则考虑该位是否存在限制（如432时，考虑最高位的 4，满足条件的只有 400～432，而如果是最高位的 3，满足条件的有 300～399）。

时间复杂度：$O(T\lg k)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

vector<int> pow10(19), pre(18);

void solve() {
    int k;
    cin >> k;
    int len = lower_bound(pre.begin() + 1, pre.end(), k) - pre.begin();
    int x = pow10[len - 1] - 1;
    k -= pre[len - 1];
    int y = k / len;
    x += y;
    k %= len;
    vector<int> dp(15, -1);
    string n = to_string(x);
    int sz = n.size();
    vector<int> now(sz + 1);
    for (int i = sz - 1; i >= 0; i--) {
        now[i] = now[i + 1] + (n[i] - '0') * pow10[sz - i - 1];
    }
    auto dfs = [&](this auto &&dfs, int pos, bool sta, bool limit) -> int {
        if (pos == sz) {
            return 0;
        }

        if (!sta && !limit && dp[pos] != -1) {
            return dp[pos];
        }

        int ans = 0;
        int up = limit ? n[pos] - '0' : 9;
        for (int i = 0; i <= up; i++) {
            if (sta && i == 0) {
                ans += dfs(pos + 1, true, limit && i == up);
            } else if (limit == true && i == up) {
                ans += i * (now[pos + 1] + 1) +
                       dfs(pos + 1, false, limit && i == up);
            } else {
                ans += i * pow10[sz - pos - 1] +
                       dfs(pos + 1, false, limit && i == up);
            }
        }

        if (!sta && !limit) {
            dp[pos] = ans;
        }
        return ans;
    };
    int ans = dfs(0, true, true);
    n = to_string(x + 1);
    for (int i = 0; i < k; i++) {
        ans += n[i] - '0';
    }
    cout << ans << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    pow10[0] = 1;
    for (int i = 1; i <= 18; i++) {
        pow10[i] = pow10[i - 1] * 10;
    }
    for (int i = 1; i < 18; i++) {
        pre[i] = pre[i - 1] + (pow10[i] - pow10[i - 1]) * i;
    }

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

P6008 [USACO20JAN] Cave Paintings P

题意

给定一个 $n\times m$ 的方格图，每个格子是墙壁，空气或水，最外一圈全部是墙壁。求将一些空白格子填上水的方案数，要求填上后不得存在水的移动（即符合连通器原理，假设方格 a 画的是水。那么如果存在一条从 a 到方格 b 的路径，由高度不超过 a 的空的方格或是有水的方格组成，路径中每相邻两个方格都有一条公共边，那么 b 画的也是水。）

题解

显然答案是若干个不相交的连通块的方案数的乘积，问题在于求单个连通块的方案数。

由于同一连通块，上方的格子放水，下面的格子也必须放水，我们从下到上一层一层地考虑。初始每个格子的方案数都是 1，第 $i$ 层的不同连通块之间互不影响，若第 $i + 1$ 层的一些空气使得第 $i$ 层的不同连通块连通起来，此时只要在第 $i+1$ 层放水，第 $i$ 层对应的连通块也全部是水，因此有 $dp_{i+1} = \prod dp_i + 1$，其中 + 1 对应第 $i + 1$ 层放水的情况，使用并查集合并即可。

最后答案就是不同连通块的乘积。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

struct DSU {
    int n;
    std::vector<int> p;
    DSU(int n_) {
        n = n_;
        init(n);
    }
    void init(int n) {
        p.resize(n + 1);
        // sz.resize(n + 1, 1);
        iota(p.begin() + 1, p.end(), 1);
    }
    int find(int x) {
        while (x != p[x]) {
            x = p[x] = p[p[x]];
        }
        return x;
    }
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        // if (sz[x] > sz[y]) {
        //     std::swap(x, y);
        // }
        // sz[y] += sz[x];
        p[x] = y;
        return true;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    // int size(int x) { return sz[find(x)]; }
};

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, m;
    cin >> n >> m;
    vector<string> a(n);
    for (int i = n - 1; i >= 0; i--) {
        cin >> a[i];
    }
    int fx[] = {0, 0, -1};
    int fy[] = {-1, 1, 0};

    auto id = [&](int x, int y) { return x * m + y; };

    vector<Z> dp(n * m, 1);
    DSU dsu(n * m);
    for (int i = 1; i < n; i++) {
        for (int j = 1; j < m - 1; j++) {
            if (a[i][j] == '#') {
                continue;
            }
            for (int z = 0; z < 3; z++) {
                int dx = i + fx[z], dy = j + fy[z];
                if (a[dx][dy] == '#') {
                    continue;
                }
                int x = dsu.find(id(i, j)), y = dsu.find(id(dx, dy));
                if (x == y) {
                    continue;
                }
                dsu.p[y] = x;
                dp[x] *= dp[y];
            }
        }
        for (int j = 1; j < m - 1; j++) {
            if (a[i][j] == '.' && dsu.find(id(i, j)) == id(i, j)) {
                dp[id(i, j)] += 1;
            }
        }
    }
    Z ans = 1;
    for (int i = 1; i < n - 1; i++) {
        for (int j = 1; j < m - 1; j++) {
            if (a[i][j] == '.' && dsu.find(id(i, j)) == id(i, j)) {
                ans *= dp[id(i, j)];
            }
        }
    }
    cout << ans << "\n";

    return 0;
}

P1350 车的放置

题意

给定一个网格图，由一个 $a\times (b + d)$ 和一个 $c\times d$ 的矩形拼接在一起，在其中放置 $k$ 个车，要求每辆车所在行和列都只有一辆，求方案数。

$a,b,c,d\le 10^3$

题解

有两种做法， dp 和直接计数。

dp 的话设 $f_{i,j}$ 为前 $i$ 行选 $j$ 个的方案数，那么 $f_{i,j} = f_{i-1,j} + f_{i-1,j - 1}\times(h_i - j + 1)$，其中 $h_i$ 代表第 $i$ 列有多少格子，注意我们应该在前 $c$ 列赋值 $h_i = d$，后 $a$ 列赋值 $h_i = b + d$，如果反过来就会漏掉一些情况，因为每一行最多放置一个，高度大的放前面会造成浪费。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 100003;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int a, b, c, d, k;
    cin >> a >> b >> c >> d >> k;
    vector f(a + c + 1, vector<Z>(k + 1));
    vector<int> h(a + c + 1);
    for (int i = 1; i <= c; i++) {
        h[i] = d;
    }
    for (int i = 1; i <= a; i++) {
        h[i + c] = d + b;
    }
    for (int i = 0; i <= a + c; i++) {
        f[i][0] = 1;
    }
    for (int i = 1; i <= a + c; i++) {
        for (int j = 1; j <= k; j++) {
            f[i][j] = f[i - 1][j] + f[i - 1][j - 1] * (h[i] - j + 1);
        }
    }
    cout << f[a + c][k] << "\n";

    return 0;
}

直接计数的话考虑以下情形：

$n\times n$ 的格子，放 $n$ 个。答案为 $n!$
$n\times n$ 的格子，放 $k$ 个。先取 $k$ 行，再在这 $k$ 行里取 $k$ 列，就转化成 $k\times k$ 放 $k$ 个了，答案为 $\begin{pmatrix}n\\k\end{pmatrix}\times \begin{pmatrix}n\\k\end{pmatrix}\times k!$
$n\times m$ 的格子，放 $k$ 个。同理，$\begin{pmatrix}n\\k\end{pmatrix}\times \begin{pmatrix}m\\k\end{pmatrix}\times k!$
本题的情形，放 $k$ 个。两个矩形可以转化为两个第三种情形的情况相乘，枚举其中一边放的个数。但是这样做会重复一些方案，为了确保不重复，设$a\times(b + d)$ 的矩形里放 $i$ 个， $c\times d$ 的矩形里放 $k - i$ 个，钦定 $cd $ 的矩形任选，那么 $a\times (b + d)$ 的矩形里，能选的行只剩下 $b + d - (k - i)$ 个。因此答案就是 $\sum_{i=0}^k\begin{pmatrix}c\\i\end{pmatrix}\begin{pmatrix}d\\i\end{pmatrix}i!\begin{pmatrix}a\\k-i\end{pmatrix}\begin{pmatrix}b+d-(k-i)\\k-i\end{pmatrix}(k-i)!$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 100003;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

struct Comb {
    int n;
    std::vector<Z> _fac;
    std::vector<Z> _invfac;
    std::vector<Z> _inv;

    Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
    Comb(int n) : Comb() { init(n); }

    void init(int m) {
        if (m <= n) return;
        _fac.resize(m + 1);
        _invfac.resize(m + 1);
        _inv.resize(m + 1);

        for (int i = n + 1; i <= m; i++) {
            _fac[i] = _fac[i - 1] * i;
        }
        _invfac[m] = _fac[m].inv();

        for (int i = m; i > n; i--) {
            _invfac[i - 1] = _invfac[i] * i;
            _inv[i] = _invfac[i] * _fac[i - 1];
        }
        n = m;
    }

    Z fac(int m) {
        if (m > n) init(2 * m);
        return _fac[m];
    }
    Z invfac(int m) {
        if (m > n) init(2 * m);
        return _invfac[m];
    }
    Z inv(int m) {
        if (m > n) init(2 * m);
        return _inv[m];
    }
    Z binom(int n, int m) {
        if (n < m || m < 0) return 0;
        return fac(n) * invfac(m) * invfac(n - m);
    }
} comb(20000);  // Z 类型全局初始化，D 类型需要局部初始化

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int a, b, c, d, k;
    cin >> a >> b >> c >> d >> k;
    Z ans = 0;
    for (int i = 0; i <= k; i++) {
        ans += comb.binom(a, i) * comb.binom(b + d - k + i, i) * comb.fac(i) *
               comb.binom(c, k - i) * comb.binom(d, k - i) * comb.fac(k - i);
    }
    cout << ans << "\n";

    return 0;
}

ABC 420 G

题意

给定 $-10^{14}\le X\le 10^{14}$，求所有 $n$，满足 $\sqrt{n^2+n+X}$ 为整数。

题解

设 $n^2 + n + X = p^2$，其中 $p$ 为整数，这个式子有平方项和一次项不方便计算，考虑合并，有 $(n + \frac{1}{2})^2 + X - \frac{1}{4} = p^2$，再利用平方差公式有 $(2p + 2n + 1)(2p - 2n - 1) = 4X - 1$，设 $4X - 1 = ab$，则 $\begin{cases}a = 2p + 2n - 1\\b = 2p - 2n - 1\end{cases}$，可以解出 $n = \frac{a - b -2}{4}$，那么我们枚举 $4X - 1$ 的因数，就能在 $O(\sqrt{n})$ 的复杂度求出所有 $n$。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int X;
    cin >> X;
    X = 4 * X - 1;
    set<int> ans;
    for (int i = 1; i * i <= abs(X); i++) {
        if (X % i == 0) {
            auto add = [&](int a) { ans.insert((a - X / a - 2) / 4); };
            add(i);
            add(-i);
            add(X / i);
            add(-X / i);
        }
    }
    cout << ans.size() << "\n";
    for (auto x : ans) {
        cout << x << " ";
    }
    cout << "\n";

    return 0;
}

CF 2133 C

题意

交互题。有一张有向无环图，你可以询问一个集合以及一个起点，返回从这个起点，只能走集合中的点的最长路径，在 $2n$ 次询问中找到一条最长路径。

题解

首先询问 $1～n$ 作为起点，点集为全集，这样可以确定答案的起点即回答路径最长对应的起点。设答案的路径长度为 $k$，那么已知起点后，下一个点一定是在询问路径长度为 $k - 1$ 的点中得到（证明：假设从长度为 $d \ge k$ 的点中得到，答案就会大于 $k$；如果从长度 $d\le k - 2$ 的点得到，答案就会小于 $k$。）这样依次询问下去，总的询问次数是 $2n - 1$ 次。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1, 1);
    auto query = [&](int x) {
        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            if (a[i]) {
                cnt++;
            }
        }
        cout << "? " << x << " " << cnt << " ";
        for (int i = 1; i <= n; i++) {
            if (a[i]) {
                cout << i << " ";
            }
        }
        cout << endl;
        int d;
        cin >> d;
        return d;
    };
    auto query2 = [&](int x, int y) {
        cout << "? " << x << " 2 " << x << " " << y << endl;
        int d;
        cin >> d;
        return d;
    };
    vector<vector<int>> id(n + 1);
    int mx = 0, s = 0;
    for (int i = 1; i <= n; i++) {
        int d = query(i);
        id[d].push_back(i);
        if (d > mx) {
            mx = d;
            s = i;
        }
    }
    vector<int> ans;
    ans.push_back(s);
    int pre = s;
    for (int i = mx - 1; i >= 1; i--) {
        for (auto x : id[i]) {
            int d = query2(pre, x);
            if (d == 2) {
                pre = x;
                ans.push_back(x);
                break;
            }
        }
    }
    cout << "! " << ans.size();
    for (auto x : ans) {
        cout << " " << x;
    }
    cout << endl;
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

CF 2133 D

题意

$n$ 个怪堆成一个塔，每个怪有 $a_i$ 的生命值，每次攻击可以造成一点伤害，一旦高度为 $h$ 的某个怪死亡，其上方所有怪会坠落，形成一个新的塔，且最下方的怪还会受到 $h$ 的坠落伤害，如果该伤害导致其死亡则重复该过程，求最小攻击次数。

题解

考虑每个怪最多受到一次坠落伤害，攻击第 $i$ 个怪时，我们要么直接杀死它，要么先让其坠落再杀死，并且如果某只怪受到的坠落伤害超过 1，一定是直接杀死了它下方的怪造成的，此时我们让其在原来的塔中杀死是最优的，而不是先让它们所在的一部分坠落后再杀死它。

设 $dp_i$ 表示杀死从低到高前 $i$ 只怪的最小攻击次数，那么有 $dp_i = \min(dp_{i-1} + a_i - 1, dp_{i - 2} + a_{i-1} + \max(0, a_i - (i - 1)))$，分别表示直接杀死第 $i$ 只和直接杀死第 $i - 1$ 只。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1), dp(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    dp[1] = a[1];
    for (int i = 2; i <= n; i++) {
        dp[i] = min(dp[i - 1] + a[i] - 1,
                    dp[i - 2] + max(0ll, a[i] - i + 1) + a[i - 1]);
    }
    cout << dp[n] << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

P3205 [HNOI2010] 合唱队

题意

定义一个新序列是由原来的序列经过以下操作得到的，给定这个新序列，满足所有元素都不相同，求有多少序列能够得到这个新序列。

操作为：首先放置第一个元素，对于后面的元素，如果比前一个元素大，就放到末尾，否则放到开头。

$n\le 1000$

题解

模数不是素数，不能用组合数来做。

考虑新放一个数，要么放在左边要么放在右边，这会拓展之前的区间，具有区间 dp 的性质。

设 $dp_{i,j,0/1}$ 是得到区间 $[i,j]$ ，且第 $i$ 个元素放在左边 / 第 $j$ 个元素放在右边的方案数，如果第 $i$ 个数放在左边，考虑上一次操作，有两种情况：若上一次操作是将第 $i + 1$ 个元素也放在左边，需要 $a_i < a_{i + 1}$，此时 $f_{i,j,0} += f_{i + 1,j ,0}$，否则不可能，如果上一次操作是第 $j$ 个元素放在右边，需要 $a_i < a_j$，此时 $f_{i,j,0} += f_{i + 1,j,1}$；如果第 $j$ 个元素放在右边，同理。

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

constexpr int N = 1005;
int dp[N][N][2];
constexpr int P = 19650827;

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++) {
        dp[i][i][0] = 1;
    }
    for (int len = 2; len <= n; len++) {
        for (int l = 1; l + len - 1 <= n; l++) {
            int r = l + len - 1;
            if (a[l] < a[l + 1]) {
                dp[l][r][0] += dp[l + 1][r][0];
            }
            if (a[l] < a[r]) {
                dp[l][r][0] += dp[l + 1][r][1];
            }
            if (a[r] > a[r - 1]) {
                dp[l][r][1] += dp[l][r - 1][1];
            }
            if (a[r] > a[l]) {
                dp[l][r][1] += dp[l][r - 1][0];
            }
            dp[l][r][0] %= P;
            dp[l][r][1] %= P;
        }
    }
    cout << (dp[1][n][0] + dp[1][n][1]) % P << "\n";

    return 0;
}

P4980 【模板】Pólya 定理

题意

给定一个 $n$ 个点，$n$ 条边的环，有 $n$ 种颜色，给每个顶点染色，问有多少种本质不同的染色方案。本质不同定义为：不能通过旋转与别的染色方案相同。

多测，$t\le 10^3, n\le 10^9$

题解

Burnside 定理

定义 $G$ 为一个置换群，定义其作用 $X$，如果 $x,y\in X$ 在 $G$ 作用下可以相等，即存在 $f\in G$ 使得 $f(x) = y$，则定义 $x,y$ 属于一个等价类，则不同的等价类数量为：$[X/G] = \frac{1}{|G|}\sum_{g\in G}X^g$。其中 $X^g$ 表示 $X$ 在 $g$ 作用下不动点的数量，即满足 $g(x) = x$ 的 $x$ 的数量。

定理的文字描述：$X$ 在群 $G$ 作用下的等价类总数等于每一个 $g$ 作用于 $X$ 的不动点数量的算术平均值。

Pólya 定理

给定群 $G$ 在集合 $X$ 上的作用和颜色集合 $C$，则不同的染色方案的数目为 $[C^X/G] = \frac{1}{|G|}\sum_{g\in G}m^{c(g)}$，其中 $c$ 为颜色数目，$c(g)$ 是元素 $g\in G$ 的置换表示的轮换分解中的轮换数目。

根据 Burnside 定理，在本题中 $G$ 代表 $\{循环左移 0,1,...,n-1\}$ 次， $m = n$，$c(g)$ 为置换 $g$ 中循环个数，也就是有多少种染色方案，循环移动 $g$ 次后不变。我们很自然地想到了循环节。对于操作循环左移 $k$ 次，考虑其中的不动点，它一定有一个周期为 $t$ 的循环节，且 $t\mid k$，并且 $t\mid n$，所以 $t\mid (n,k)$。如果 $t\ne (n,k)$，我们就可以构造一个 $k^\prime < k$ 使得 $t = (n, k^\prime)$。为了保证枚举不重复，我们不妨令 $t = (n,k)$，这 $(n,k)$ 个位置也可以任意排布，共有 $n^{(n,k)}$ 种方式，即 $|X^g| = n^{(n,k)}$ 。

因此，答案就是 $\frac{1}{n}\sum_{k=1}^nn^{(n,k)}$。如果使用 Pólya 定理，实际上循环节也对应着循环置换，$(n,k)$ 就是把置换 $g$ 拆分成的不相交的循环置换的数量。

在该数据范围下，还需要进一步推导该式子： \[ \begin{align*} &\frac{1}{n}\sum_{k=1}^nn^{(n,k)}\\\\ &=\frac{1}{n}\sum_{d\mid n}n^d\sum_{k=1}^n[(n,k)=d]\\\\ &=\frac{1}{n}\sum_{d\mid n}n^d\sum_{k=1}^{\lfloor\frac{n}{d}\rfloor}[(\frac{n}{d},k)=1]\\\\ &=\frac{1}{n}\sum_{d\mid n}n^d\varphi(\frac{n}{d}) \end{align*} \] 时间复杂度 $O(Tn^{\frac{3}{4}})$，比较勉强但是过了（

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

int phi(int n) {
    int res = n;
    for (int i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            while (n % i == 0) {
                n /= i;
            }
            res = res / i * (i - 1);
        }
    }
    if (n > 1) {
        res = res / n * (n - 1);
    }
    return res;
}

void solve() {
    int n;
    cin >> n;
    Z ans = 0;
    for (int i = 1; i * i <= n; i++) {
        if (n % i) {
            continue;
        }
        ans += phi(n / i) * power(Z(n), i);
        if (n / i != i) {
            ans += phi(i) * power(Z(n), n / i);
        }
    }
    cout << ans / n << "\n";
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }

    return 0;
}

P1446 [HNOI2008] Cards

题意

将 $n$ 张牌染成恰好 $S_r$ 张红色，$S_g$ 张绿色，$S_b$ 张蓝色，给定 $m$ 种洗牌方式（置换），求有多少本质不同的染色方案。本质相同定义为一种染色能通过另一种染色若干次洗牌得到。

$S_r,S_g,S_b\le 20,m\le 60$

题解

置换想到 Burnside 定理，这里 $G$ 就是给定的 $m$ 种置换，$|X^g|$ 就是经过置换 $g$ 后本质相同的方案数（不动点数量），而每种置换，通过 $i$ 向 $p_i$ 连边会得到若干个环，每个环为不动点的话，需要颜色相同，而在题目中的颜色限制下，我们可以 dp 求出对应的方案数。

设 $dp_{t,i,j,k}$ 为前 $t$ 个环，用了 $i$ 种红色，$j$ 种绿色，$k$ 种蓝色的方案数，那么设 $sz_t$ 为第 $t$ 个环的大小，有 $dp_{t,i,j,k} = dp_{t-1,i - sz_t,j,k} + dp_{t-1,i, j - sz_t,k} + dp_{t-1,i,j,k - sz_t}$。

注意 1,2,3,...,n 也要算一个置换。

时间复杂度：$O(m^2S_rS_gS_b)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

D dp[21][21][21];

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int r, g, b, m, P;
    cin >> r >> g >> b >> m >> P;
    D::setMod(P);
    D ans = 0;
    int n = r + g + b;
    vector<int> p(n + 1);
    iota(p.begin(), p.end(), 0);
    auto get = [&]() {
        vector<bool> vis(n + 1);
        vector<int> l(1);
        for (int i = 1; i <= n; i++) {
            if (!vis[i]) {
                int j = i;
                int cnt = 0;
                while (!vis[j]) {
                    vis[j] = true;
                    j = p[j];
                    cnt++;
                }
                l.push_back(cnt);
            }
        }
        int sz = l.size();
        for (int i = 0; i <= r; i++) {
            for (int j = 0; j <= g; j++) {
                for (int k = 0; k <= b; k++) {
                    dp[i][j][k] = 0;
                }
            }
        }
        dp[0][0][0] = 1;
        for (int t = 1; t < sz; t++) {
            for (int i = r; i >= 0; i--) {
                for (int j = g; j >= 0; j--) {
                    for (int k = b; k >= 0; k--) {
                        if (i >= l[t]) {
                            dp[i][j][k] += dp[i - l[t]][j][k];
                        }
                        if (j >= l[t]) {
                            dp[i][j][k] += dp[i][j - l[t]][k];
                        }
                        if (k >= l[t]) {
                            dp[i][j][k] += dp[i][j][k - l[t]];
                        }
                    }
                }
            }
        }
        return dp[r][g][b];
    };
    ans += get();
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> p[j];
        }
        ans += get();
    }
    ans /= m + 1;
    cout << ans << "\n";

    return 0;
}

P1450 [HAOI2008] 硬币购物

题意

有四种硬币，面值为 $c_i$，$n$ 次询问，每次询问购买价值 $s$ 的东西，四种硬币各有 $d_i$ 种，求有多少种付款方式。

$n\le 1000,c_i,d_i,s\le 10^5$

题解

容斥原理：容斥原理常用于集合的计数问题，而对于两个集合的函数 $f(S),g(S)$，若 $f(S) = \sum_{T\subseteq S}g(T)$，则 $g(S) = \sum_{T\subseteq S}(-1)^{|S| - |T|}f(T)$。还有一种推论是若 $f(S) = \sum_{S\subseteq T}g(T)$，则 $g(S) = \sum_{S\subseteq T}(-1)^{|T|-|S|}g(T)$。

如果没有四种硬币的限制，可以采用完全背包来算方案数，复杂度 $O(4s)$。

现在考虑限制一种硬币，两种硬币，三种硬币，四种硬币的情况，可以使用容斥原理来算。

设 $f(S)$ 为 $S$ 中所有元素超出上限的方案数，$g(S)$ 为恰好 $S$ 中所有元素超出上限的方案数，注意区别：$f(S)$ 中可能存在不在 $S$ 中的元素，仍然超出上限。那么 $f(S) = \sum_{S\subseteq T}g(T)$，答案就是 $g(\varnothing) = \sum_{S}(-1)^{|S|}f(S)$，现在考虑怎么算 $f(S)$。

假设第 $x$ 种硬币超出上限，那么它至少拿了 $d_x + 1$ 个，我们将其从总金额减去就是没有上限的情况数，可以通过完全背包预处理。可以使用二进制枚举集合。

时间复杂度：$O(4s + 64n)$

Lutece 3197

题意

用 $s$ 元买 $n$ 种物品，第 $i$ 种物品有 $d_i$ 个，每种物品的价格都是 1 元，求购买方案对 $10^9 + 7$ 取模。

$s,d_i\le10^{14},n\le 20$

题解

跟上一题非常类似，设 $f(S)$ 为 $S$ 中所有元素超出上限的方案数，$g(S)$ 为恰好 $S$ 中所有元素超出上限的方案数，那么 $f(S) = \sum_{S\subseteq T}g(T)$，答案就是 $g(\varnothing) = \sum_{S}(-1)^{|S|}f(S)$，现在考虑怎么算 $f(S)$。

考虑一个经典的球盒模型：$n$ 个相同的元素分成 $k$ 组，每组允许为空的方案数。如果不允许为空就是插板法，拿 $k - 1$ 块板子插入 $n - 1$ 个空，即 $\begin{pmatrix}n - 1\\k - 1\end{pmatrix}$，如果允许为空，可以先借 $k$ 个元素，使得每一组都有一个元素，在这些数形成的 $n + k - 1$ 个空里插板，即 $\begin{pmatrix}n +k - 1\\k - 1\end{pmatrix}$。

这里如果所有元素都可以超出上限（都有无数个），就是把 $s$ 个元素分成 $n$ 类，每类可以为空，答案就是 $\begin{pmatrix}s +n - 1\\n - 1\end{pmatrix}$，再考虑强制集合 $S$ 中元素超出上限，和上一题类似，答案就是 $\begin{pmatrix}s +n - \sum_{i\in S}(d_i + 1)- 1\\n - 1\end{pmatrix}$。

这里由于 $s$ 很大，$n$ 很小，求组合数直接算下降幂和阶乘，复杂度 $O(n)$

#include <bits/stdc++.h>

#define int long long
using namespace std;

using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

using u128 = unsigned __int128;
using i128 = __int128;
using ld = long double;

template <class T>
constexpr T power(T a, i64 b) {
    T res = 1;
    for (; b; b /= 2, a *= a) {
        if (b % 2) {
            res *= a;
        }
    }
    return res;
}

constexpr i64 mul(i64 a, i64 b, i64 p) {
    i64 res = a * b - i64(1.L * a * b / p) * p;
    res %= p;
    if (res < 0) {
        res += p;
    }
    return res;
}
template <int P>
struct MInt {
    int x;
    constexpr MInt() : x{} {}
    constexpr MInt(i64 x) : x{norm(x % getMod())} {}

    static int Mod;
    constexpr static int getMod() {
        if (P > 0) {
            return P;
        } else {
            return Mod;
        }
    }
    constexpr static void setMod(int Mod_) { Mod = Mod_; }
    constexpr int norm(int x) const {
        if (x < 0) {
            x += getMod();
        }
        if (x >= getMod()) {
            x -= getMod();
        }
        return x;
    }
    constexpr int val() const { return x; }
    explicit constexpr operator int() const { return x; }
    constexpr MInt operator-() const {
        MInt res;
        res.x = norm(getMod() - x);
        return res;
    }
    constexpr MInt inv() const {
        assert(x != 0);
        return power(*this, getMod() - 2);
    }
    constexpr MInt &operator*=(MInt rhs) & {
        x = 1LL * x * rhs.x % getMod();
        return *this;
    }
    constexpr MInt &operator+=(MInt rhs) & {
        x = norm(x + rhs.x);
        return *this;
    }
    constexpr MInt &operator-=(MInt rhs) & {
        x = norm(x - rhs.x);
        return *this;
    }
    constexpr MInt &operator/=(MInt rhs) & { return *this *= rhs.inv(); }
    friend constexpr MInt operator*(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res *= rhs;
        return res;
    }
    friend constexpr MInt operator+(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res += rhs;
        return res;
    }
    friend constexpr MInt operator-(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res -= rhs;
        return res;
    }
    friend constexpr MInt operator/(MInt lhs, MInt rhs) {
        MInt res = lhs;
        res /= rhs;
        return res;
    }
    friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {
        i64 v;
        is >> v;
        a = MInt(v);
        return is;
    }
    friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {
        return os << a.val();
    }
    friend constexpr bool operator==(MInt lhs, MInt rhs) {
        return lhs.val() == rhs.val();
    }
    friend constexpr bool operator!=(MInt lhs, MInt rhs) {
        return lhs.val() != rhs.val();
    }
};
template <>
int MInt<0>::Mod = 998244353;

template <int V, int P>
constexpr MInt<P> CInv = MInt<P>(V).inv();

constexpr int P = 1000000007;
using Z = MInt<P>;  // 静态模数，题目给定模数
using D = MInt<0>;  // 动态模数，可以 D::setMod(x) 改变

Z comb(int n, int m) {
    Z a1 = 1, a2 = 1;
    for (int i = 1; i <= m; i++) {
        a1 *= (n - i + 1);
        a2 *= i;
    }
    return a1 / a2;
}

signed main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int n, s;
    cin >> n >> s;
    vector<int> d(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> d[i];
    }
    int S = 1 << n;
    Z ans = 0;
    for (int i = 0; i < S; i++) {
        int cnt = 1;
        int sum = n + s - 1;
        for (int j = 1; j <= n; j++) {
            if (i >> (j - 1) & 1) {
                cnt *= -1;
                sum -= d[j] + 1;
            }
        }
        if (sum < 0) {
            continue;
        }
        ans += cnt * comb(sum, n - 1);
    }
    cout << ans << "\n";

    return 0;
}