组合数学学习笔记

发表于 2025-08-28 更新于 2025-09-09 分类于 Algorithm 阅读次数：本文字数： 7.9k

苦练计数。

组合恒等变换

组合数

$\begin{pmatrix}n\\m\end{pmatrix}$ 读作 “$n$ 选 $m$”，$\begin{pmatrix}n\\m\end{pmatrix} =\displaystyle \frac{n(n-1)...(n - m + 1)}{m(m - 1)...1} = \frac{n!}{m!(n - m)!}$。

可以定义广义二项式系数：$\begin{pmatrix}r\\k\end{pmatrix}=\begin{cases}\frac{r(r-1)...(r-k+1)}{k(k-1)...1} = \frac{r^{\underline{k}}}{k!},&整数k\ge 0\\0, &整数 k < 0\end{cases}$，这里 $r$ 为非负整数时，就退化为普通二项式系数，$r$ 为负数或非整数时，仍然可以按照公式计算。

求组合数的几种方法

预处理阶乘及逆元：预处理 $O(n)$，查询 $O(1)$
当 $n$ 很小，或者题目没有给定模数，用加法公式预处理（可能用到高精度），预处理 $O(n^2)$，查询 $O(1)$。
当 $m$ 很小，通过 $\begin{pmatrix}n\\m\end{pmatrix} = \frac{n^{\underline{m}}}{m!}$ 暴力计算（可以预处理分母），预处理 $O(m)$，查询 $O(m)$
当模数 $P$ 很小，根据 Lucas 定理，$\begin{pmatrix}n\\m\end{pmatrix}\equiv \begin{pmatrix}n\mod p\\m\mod p\end{pmatrix}\begin{pmatrix}\lfloor\frac{n}{p}\rfloor\\\lfloor\frac{m}{p}\rfloor\end{pmatrix}\pmod P$预处理 $O(P^2)$，查询 $O(\log_Pn)$。

组合恒等变换

对称性

$\begin{pmatrix}n\\m\end{pmatrix} = \begin{pmatrix}n\\n - m\end{pmatrix}$，整数 $n\ge 0$，$m$ 是整数。

二项式定理

当 $n\le 0$ 且 $n$ 为整数时，是最常见的情况：$(x+y)^n = \sum_{k=0}^n\begin{pmatrix}n\\k\end{pmatrix}x^ky^{n-k}$。

当 $|\frac{y}{x}|\le 1$ 时，$n$ 可以是任意实数或复数，这是广义二项式展开的条件，即 Newton 二项式公式：$(x+y)^n=\sum_{k=0}^\infin\begin{pmatrix}n\\k\end{pmatrix}x^{n-k}y^k$，其中 $\begin{pmatrix}n\\k\end{pmatrix}$ 也是广义二项式系数。

吸收恒等式

$k\begin{pmatrix}r\\k\end{pmatrix} = r\begin{pmatrix}r-1\\k-1\end{pmatrix}$，$k$ 是整数。将组合数展开为阶乘即可推导。

推论：$(r - k)\begin{pmatrix}r\\k\end{pmatrix} = r\begin{pmatrix}r - 1\\k\end{pmatrix}$，$k$ 是整数。因为 $r\begin{pmatrix}r-1\\k\end{pmatrix}=(k+1)\begin{pmatrix}r\\k+1\end{pmatrix} = (r-k)\begin{pmatrix}r\\k\end{pmatrix}$。

加法公式

$\begin{pmatrix}r\\k\end{pmatrix} = \begin{pmatrix}r - 1\\k - 1\end{pmatrix} + \begin{pmatrix}r - 1\\k\end{pmatrix}$，$k$ 是整数。通过杨辉三角的意义即可推导。

平行求和法

$\sum_{k\le n}\begin{pmatrix}r+k\\k\end{pmatrix} = \begin{pmatrix}r\\0\end{pmatrix} + \begin{pmatrix}r+1\\1\end{pmatrix} + ... + \begin{pmatrix}r+n\\n\end{pmatrix} = \begin{pmatrix}r + n + 1\\n\end{pmatrix}$，$n$ 是整数。注意没有 $r$ 的限制，可以推广到广义二项式系数。

如图，这个式子表示第 $r$ 行（0-index）开始取 $n + 1$ 个数，杨辉三角的斜线和，通过加法公式可以推导出就是最后一个数的下面一个位置的值。

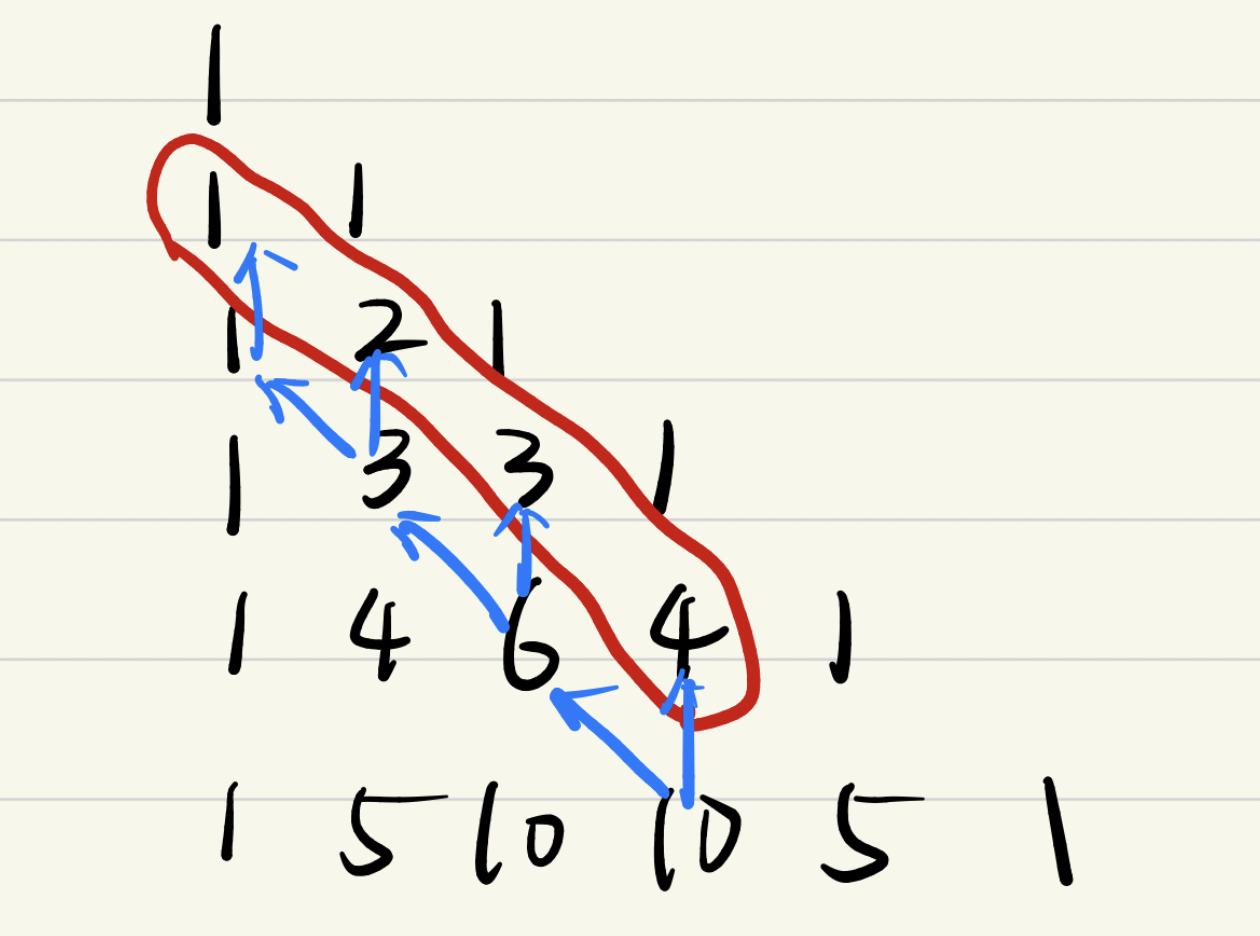
上指标求和法

$\sum_{0\le k\le n}\begin{pmatrix}k\\m\end{pmatrix} = \begin{pmatrix}0\\m\end{pmatrix} + \begin{pmatrix}1\\m\end{pmatrix} + ... + \begin{pmatrix}n\\m\end{pmatrix} = \begin{pmatrix}n + 1\\m + 1\end{pmatrix}$，整数 $m,n\ge 0$。

如图，这个式子就是杨辉三角一列的和（开头必须是 1），通过加法公式可以推导出就是最后一个数右下角。

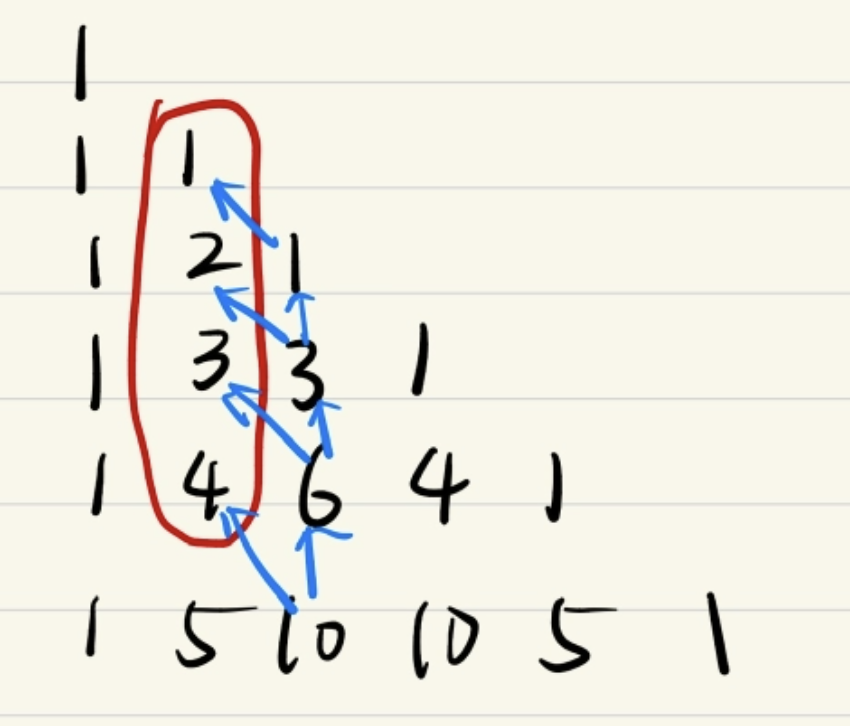
上指标反转

$\begin{pmatrix}r\\k\end{pmatrix} = (-1)^k\begin{pmatrix}k - r - 1\\k\end{pmatrix}$，$k$ 是整数。

根据广义二项式系数，$\begin{pmatrix}k - r - 1\\k\end{pmatrix} = \displaystyle\frac{(k-r-1)(k-r-2)...(-r)}{k!} = \frac{(-1)^kr(r-1)...(r-k+1)}{k!}$。

三项式版恒等式

$\begin{pmatrix}r\\m\end{pmatrix} \begin{pmatrix}m\\k\end{pmatrix}= \begin{pmatrix}r\\k\end{pmatrix}\begin{pmatrix}r-k\\m-k\end{pmatrix}$。

考虑组合意义，即左边的意义是先选 $m$ 个元素，再从这 $m$ 个元素里选 $k$ 个。右边的意义是先选 $k$ 个元素，再从剩下的 $r-k$ 个元素中选 $m-k$ 个。

三项式系数

$\begin{pmatrix}a+b+c\\a,b,c\end{pmatrix} = \displaystyle\frac{(a+b+c)!}{a!b!c!} = \begin{pmatrix}a+b+c\\b+c\end{pmatrix}\begin{pmatrix}b+c\\c\end{pmatrix}$。

表示从 $a+b+c$ 个元素中选出 $a$ 个放在第一类，$b$ 个放在第二类，$c$ 个放在第三类的方案数。

同理，可以推广到多项式系数。

范德蒙徳卷积

$\sum_{k}\begin{pmatrix}r\\k\end{pmatrix}\begin{pmatrix}s\\n-k\end{pmatrix} = \begin{pmatrix}r+s\\n\end{pmatrix}$。考虑组合意义，从两个集合中一共选 $n$ 个的方案数，就是枚举在第一个集合中选 $k$ 个的方案数，乘上在第二个集合中选 $n - k$ 个的方案数。

特殊的数

错位排列

定义 $D_n$ 为有多少个长度为 $n$ 的排列 $P$ 满足 $P_i \ne i$。

有递推公式：$D_n = (n - 1)(D_{n - 1} + D_{n - 2})$。含义是：在 $D_{n-1}$ 的基础上加第 $n$ 个数，那么把 $P_n$ 跟前面任意一个位置交换即可，或者前面 $n - 1$ 个数有一个位置满足 $P_i = i$，那么新增一个数后，让 $P_i$ 和 $P_n$ 互换位置即可。

初值 $D_1 = 0, D_2 = 1$。

卡特兰数

卡特兰数对应序列为：$H_0 = 1, H_1 = 1, H_2 = 2, H_3 = 5,H_4 = 14, H_5=42,H_6=132,...$。

应用于以下问题：

$2n$ 个人排成一行进入剧场，入场费 5 元，其中 $n$ 个人只有一张 5 元，另外 $n$ 人只有一张 10 元，剧院无其他钞票，求有多少种方法使得只要有 10 元钞票，售票处就有 5 元的钞票找零。
有一个大小为 $n\times n$ 的方格图，左下角 $(0,0)$，右下角 $(n,n)$。从左下角开始每次都只能向右或者向上一个单位，不走到对角线 $y = x$ 上方（但可以触碰）的情况下到达右上角的方案数。
在圆上选择 $2n$ 个点，将这些点成对连接起来使得得到的 $n$ 条线段不相交的方案数。
对角线不相交的情况下，将一个凸多边形分成三角形区域的方案数。
一个栈的进栈序列为 $1,2,3,...,n$，求有多少种不同的出栈序列。
$n$ 个节点可以构造多少个不同的二叉树。
由 $n$ 个 +1 和 $n$ 个 -1 组成的 $2n$ 个数 $a_1,a_2,...,a_{2n}$，其部分和满足 $a_1+a_2+...+a_k\ge 0,k=1,2,3,...,2n$，有多少个满足条件的数列。

以上问题的答案均是卡特兰数 $H_i$。卡特兰数有几个常见公式，可以对应上述情况：

$H_n = \begin{cases}\sum_{i=1}^nH_{i-1}H_{n-i}&n\ge 2,n\in N_+\\1&n=0,1\end{cases}$

$H_n = \displaystyle\frac{H_{n-1}(4n-2)}{n+1}$

$H_n = \begin{pmatrix}2n\\n\end{pmatrix} - \begin{pmatrix}2n\\n - 1\end{pmatrix}$

例如，我们处理问题 3，我们将圆顺时针编号 $1,2,...,2n$，选择一个固定点 1，他必须与一个偶数编号的点配对，我们将这条线段画出后，圆被分成上下两部分，也就是拆成两个子问题。若弦一侧含有 $2k$ 个点，就能组成 $k$ 对，枚举 $k = 0,1,2,...,n-1$ 得到递推 $C_n = \sum_{k=0}^{n-1}C_{k}C_{n-1-k}$，符合卡特兰数的形式，初值 $C_0 = 1$。

我们还可以给卡特兰数抽象出这样一种数学模型：对于一个只含有两种操作（设为操作1，操作2）的问题，问题的解是由这两种操作构成的排列，并且操作1的总数等于操作2的总数，任取前 $k$ 项（$k\ge1$），若满足操作 1 的个数大于等于操作 2 的个数才是问题的一种解，则问题解的个数就是卡特兰数。

折线法

卡特兰数的代数推导非常麻烦，用折线法来证明却让人豁然开朗，下面是折线法证明 $H_n = \begin{pmatrix}2n\\n\end{pmatrix} - \begin{pmatrix}2n\\n - 1\end{pmatrix}$ 的过程：

考虑问题 1 的情景，我们在二维坐标系下画折线，如果一个人是拿着 5 元钞票的话就向右上 $45\degree$ 方向画折线，否则向右下 $45\degree$ 方向画，长度都是一个单位。这样，题目的限制就转化成了，不能到达 $y = -1$。

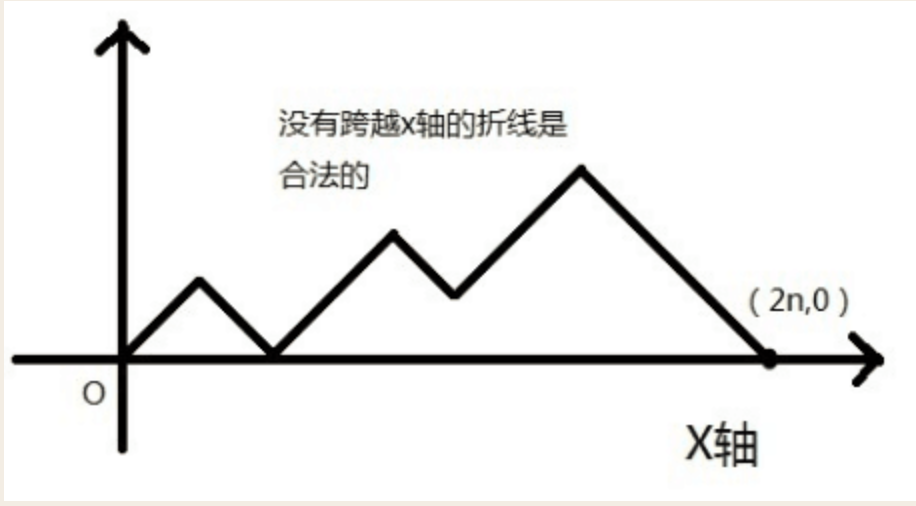
那么，如果没有限制，总方案数就是 $\begin{pmatrix}2n\\n\end{pmatrix}$，代表从 $2n$ 步中任取 $n$ 步作为操作一。

考虑存在限制的情况，任何一条路径都会回到 $(2n,0)$，而不合法的会到达 $y = -1$。我们这路径第一次与 $y = -1$ 的交点为 $k$，我们将 $k$ 点右方的路径关于 $y = -1$ 翻折，含义就是将这点后续的操作一和操作二对换。这样，路径会到达 $(2n,-2)$，如图：

由于对称总是能进行的且是可逆的，因此不合法的折线总数转化成了从 $(0,0)$ 到 $(2n,-2)$ 折线的总数，相当于 $2n$ 步中取 $n - 1$ 次操作一，$n + 1$ 次操作二，不合法的方案数就是 $\begin{pmatrix}2n\\n - 1\end{pmatrix}$。

因此，总方案数就是 $\begin{pmatrix}2n\\n\end{pmatrix} - \begin{pmatrix}2n\\n-1\end{pmatrix}$。

通过折线法，我们还可以解决一些路径计数问题。

我们定义非降路径是只能向上或向右走的路径。

从 $(0,0)$ 走到 $(m,n)$ 的非降路径数等于 $m$ 个 $x$ 和 $n$ 个 $y$ 的排列数，即 $\begin{pmatrix}n+m\\n\end{pmatrix}$
从 $(0,0)$ 走到 $(n,n)$ 的除端点外不接触直线 $y = x$ 的非降路径数。我们先考虑 $y = x$ 下方的路径，此时第一步一定是走到 $(1,0)$，最后一步一定是从 $(n,n-1)$ 走到 $(n,n)$，那么等价于从 $(1,0)$ 到 $(n,n-1)$ 全程不触碰 $y=x$ 的路径数，这里可以采用折线法，无限制的话方案就是 $\begin{pmatrix}2n - 2\\n - 1\end{pmatrix}$，再考虑触碰到 $y = x$，在将一个交点之后的路径对称，等价于走到 $(n-1,n)$ 的方案数，即 $\begin{pmatrix}2n-2\\n - 2\end{pmatrix}$。因此 $y = x$ 下方的方案数就是 $\begin{pmatrix}2n - 2\\n - 1\end{pmatrix} - \begin{pmatrix}2n-2\\n - 2\end{pmatrix}$。而 $y = x$ 上方完全对称，总方案数就是 $2\begin{pmatrix}2n - 2\\n - 1\end{pmatrix} - 2\begin{pmatrix}2n-2\\n - 2\end{pmatrix}$。
从 $(0,0)$ 到 $(n,n)$ 的除端点外不穿过直线 $y = x$ 的方案数。和上一题类似，先考虑 $y = x$ 下方的路径，此时“不穿过”等价于不接触 $y = x + 1$，同理可以推出总方案数就是 $2\begin{pmatrix}2n \\n \end{pmatrix} - 2\begin{pmatrix}2n\\n - 1\end{pmatrix} = \displaystyle \frac{2}{n+1}\begin{pmatrix}2n \\n \end{pmatrix}$。

第二类斯特林数

第二类斯特林数 $\left\{\begin{matrix}n\\k\end{matrix} \right\}$，也可记作 $S(n,k)$，表示将 $n$ 个两两不同的元素，划分为 $k$ 个互不区分的非空子集的方案数。

递推式：$\left\{\begin{matrix}n\\k\end{matrix} \right\} = \left\{\begin{matrix}n - 1\\k - 1\end{matrix} \right\} + k\left\{\begin{matrix}n- 1\\k\end{matrix} \right\}$，边界是 $\left\{\begin{matrix}n\\0\end{matrix} \right\} = [n = 0]$。

通过组合意义来证明：插入一个新元素时，有两种方案：将新元素单独放入一个子集，有 $\left\{\begin{matrix}n-1\\k-1\end{matrix} \right\}$ 种方案；将新元素放入一个现有的非空子集，有 $k\left\{\begin{matrix}n - 1\\k\end{matrix} \right\}$ 种方案。根据加法原理，二者相加即可得到递推式。

根据这个递推式，可以 $O(n^2)$ 预处理。

同时，第二类斯特林数具有通项公式：$\left\{\begin{matrix}n\\m\end{matrix} \right\} = \sum_{i=0}^m\displaystyle\frac{(-1)^{m-i}i^n}{i!(m-i)!}$。预处理阶乘后，可以 $O(n\log n)$ 求出单个第二类斯特林数。

注意到通项公式中含有 $i^n$，这启示我们当题目所求和式带有 $i^n$ 项时，可以考虑将其展开为第二类斯特林数，即 $i^n = \sum_{k=0}^n\left\{\begin{matrix}n\\k\end{matrix} \right\}i^{\underline{k}}$。

容斥及反演

容斥原理

就是将一般的“$x$ 人喜欢语文，$y$ 人喜欢数学，$z$ 人喜欢英语，求至少喜欢一门课的人数” 推广一下。

容斥原理常用于集合的计数问题，对于两个集合的函数 $f(S),g(S)$，若 $f(S) = \sum_{T\subseteq S}g(T)$，则 $g(S) = \sum_{T\subseteq S}(-1)^{|S| - |T|}f(T)$。还有一种推论是若 $f(S) = \sum_{S\subseteq T}g(T)$，则 $g(S) = \sum_{S\subseteq T}(-1)^{|T|-|S|}g(T)$。

反演

简单理解一下反演，如果能够从 $f$ 推出 $g$，则称之为正演，那么反过来通过 $g$ 推出 $f$ 就是反演。

二项式反演

如果有 $g_n = \sum_{i=0}^n\begin{pmatrix}n\\i\end{pmatrix}f_i$，那么 $f_n = \sum_{i=0}^n\begin{pmatrix}n\\i\end{pmatrix}(-1)^{n-i}g_i$。

上面这对式子就是二项式反演。还有变式：若 $F(n) = \sum_{i=n}^m\begin{pmatrix}i\\n\end{pmatrix}G(i)$，则 $ G(n) = _{i=n}^m(-1){i-n} \[\begin{pmatrix}i\\n\end{pmatrix}\]

F(i)$

Min-Max 反演

对于满足全序关系并且其中元素满足可加减性的序列 $\{x_i\}$，设其长度为 $n$，并设 $S = \{1,2,3,...,n\}$，则有：

$\displaystyle \max_{i\in S}x_i = \sum_{T\subseteq S}(-1)^{|T| - 1}\min_{j\in T}x_j$

$\displaystyle \min_{i\in S}x_i = \sum_{T\subseteq S}(-1)^{|T| - 1}\max_{j\in T}x_j$

组合数学学习笔记

组合恒等变换

组合数

求组合数的几种方法

组合恒等变换

特殊的数

错位排列

卡特兰数

折线法

第二类斯特林数

容斥及反演

容斥原理

反演

二项式反演

Min-Max 反演

例题

CF 938 E

P3266 [JLOI2015] 骗我呢

CF 932 E

CF 1278 F

计蒜客 T2766